●論理的思考の意味

　本連載【第１回】「論理的思考で視野を広げよう！」では、「論理的思考」が「思考の筋道を整理して明らかにする」ことであると解説した。たとえば「男女の三角関係」のように複雑な問題であっても、思考の筋道を整理して明らかにしていく過程で、発想の幅が広がり、それまで気づかなかった新たな論点が見えてくる思考法である。
　【第2回】「論理的思考で自分の価値観を見極めよう！」では、「ロジカルコミュニケーション」によって新たな論点を探し、反論にも公平に耳を傾け、最終的に自分がどの論点を重視しているのか、自分自身の価値観を見極めることの意義を説明した。
　【第3回】「論点のすりかえは止めよう！」では、「ロジカルコミュニケーション」の大きな障害になる10の代表的な「論点のすりかえ」について具体的に紹介した。日常的にできる限り論点のすりかえを止めるだけでも、コミュニケーションはかなりスムーズで建設的になるはずである。
　【第4回】「白黒論法に注意しよう！」では、とくに詐欺師がよく使う「白」か「黒」しか選択の余地がないと思わせる「白黒論法」を解説した。相手が「白黒論法」のような「二分法」を押し付けてきた場合、命題を整理すると実際の組み合わせは2通りではなく4通りであることが多いことに注意してほしい。

●否定「Pではない」（￢P）

　今回のテーマは「論理的結合子（logical connectives）」である。というと難しく聞こえるかもしれないが、日常言語では、ごく普通に文と文を「接続詞」で結合させて、文章を膨らませている。それを論理的に厳密に考えてみるとどうなるか、という話である。

　すでに本連載【第4回】で説明したように、Pが命題であれば「Pではない」も命題である。論理学では「Pではない」をPの「否定（negation）」と呼び、記号では「￢P」のように表す。
　このとき、Pが「真」（T: True）であれば「Pではない」は「偽」（F: False）であり、Pが偽であれば「Pではない」は真であることは明らかだろう。

　このように、「命題」と「論理的結合子」を組み合わせて、可能な「真理値」（TかF）の情報を記入した表を「真理表」（truth table）と呼ぶ。

　たとえば、P=「今日は日曜日である」とすると￢P=「今日は日曜日ではない」である。
　P=「今日は日曜日である」が真（T）であれば￢P=「今日は日曜日ではない」は偽（F）であり、P=「今日は日曜日である」が偽（F）であれば￢P=「今日は日曜日ではない」は真（T）である。

　ここで注意してほしいのは、Pと￢Pが必ずしも対等ではないという点である。
　P=「今日は日曜日である」であれば、Pを真にさせるためには、今日は日曜日でなければならない。ところが、￢P=「今日は日曜日ではない」を真にさせるためには、今日は月曜日・火曜日・水曜日・木曜日・金曜日・土曜日のどれでも構わない。つまりPは1通りしかないが、￢Pには6通りの可能性があることになる。
　Q＝「この紙は白である」であれば、Qを真にさせるためには、この紙は白でなければならない。ところが、￢Q=「この紙は白ではない」を真にさせるためには、この紙が白以外の赤・青・黄・緑色など、実際には無数の白以外の色で構わないわけである。
　R＝「この碁石は白である」とすると、￢R＝「この碁石は白ではない」となり、それはすなわち「この碁石は黒である」になる。碁石には「白」か「黒」しかないため、白でなければ黒、黒でなければ白が成り立つためである。このように特殊な条件を満たす場合に限って、Rと￢Rは対等になる。

●連言「PかつQ」（P∧Q）

　PとQが命題であれば、「PかつQ」も命題である。論理学では「PかつQ」をPとQの「連言（conjunction）」と呼び、記号では「P⋀Q」のように表す。この命題は、Pが真であると同時にQが真であるときに限って真であり、それ以外の場合は、偽と定義される。

　たとえば、P=「今日は月曜日である」、Q＝「今日は論理学の授業がある」であれば、「PかつQ」は「今日は月曜日であり、かつ今日は論理学の授業がある」になる。
　この「PかつQ」という命題は、P=「今日は月曜日である」が真であり、Q＝「今日は論理学の授業がある」も真である場合に限って真になる。つまり、今日が月曜日であり、論理学の授業がある場合に限って真になり、それ以外の場合は偽になる。

　さて、世界の多くの国々では「筆記試験」と「実技試験」の両方に合格しなければ、運転免許証を取得できないのが普通である。論理的には、P＝「筆記試験に合格する」かつQ＝「実技試験に合格する」の両方を満たす場合に限って、運転免許証を取得できることになる。
　別の例を挙げよう。もし医者から「薬Pかつ薬Qを朝食後に飲んでください」と指示されたら、患者は薬Pと薬Qの両方を朝食後に飲まなければならない。薬Pだけ、あるいは薬Qだけを飲んでも不十分である。もちろん、両方を飲まない場合も不十分であることは明らかだろう。

　要するに「PかつQ」を成立させるためには、PとQの両方が真でなければならないのである。

●リンダ問題

　ここで読者に次の問題を考えてほしい。

　リンダという女性がいる。彼女は、31歳で独身である。非常に聡明で、ハッキリとものを言う性格である。大学時代は哲学を専攻し、とくに社会における正義と女性差別の問題を追究してきた。実際の社会活動にも深く関わり、核兵器反対のデモに参加したこともある。さて、リンダの現在を推測する場合、どちらの可能性が高いだろうか？

A：「リンダは銀行の窓口係である」
B：「リンダは銀行の窓口係であり、フェミニスト活動家である」

　この問題を論理的に分析してみよう。
　ここでP＝「リンダは銀行の窓口係である」、Q＝「リンダはフェミニスト活動家である」とおくと、A＝「P」であり、B＝「PかつQ」であることがわかる。
　つまり、BはAに含まれる（集合論をご存知であれば「BはAの部分集合」）わけだから、明らかにBよりもAの可能性のほうが高い。したがって、解答は「Aの可能性が高い」となる。

　論理的に「P」、「PかつQ」、「PかつQかつR」と連言が増えていけばいくほど選択肢の数が狭まることは、ネットの「検索」を考えてみるとわかりやすいだろう。
　たとえば、ネットの検索で「レストラン」、「銀座にあるレストラン」、「銀座にあるイタリアンのレストラン」と絞り込んでいけばいくほど、選択肢の数が減っていくことは、読者が何度も経験しているはずである。
　逆に言えば、リンダ問題では「銀行の窓口係」の方が「銀行の窓口係かつフェミニスト活動家」よりも遥かに可能性が高いわけである。

　ところが、実際に大学の授業で尋ねてみると、Bの可能性の方が高いと錯覚してしまう学生が多い。数学が得意なはずの理学部や工学部の学生でさえ間違うことが多いのだが、それはなぜだろうか？
　その理由は、人間の判断に潜む「代表的ヒューリスティック」にあると考えられる。「ヒューリスティック」とは「発見的手法」という意味だが、非常に単純化してわかりやすくいうと、いわゆる「直感」のことである。
　たとえば、読者が初対面の人物と会った際、この人は信用できそうだとか、逆に信用できないのではないかなどと「直感的」に判断することがあるだろう。なぜか言葉ではうまく明確に表現できないが、読者は、これまでの経験から「直感的」つまり「ヒューリスティック」に相手を判断しているわけである。
　そして、この「ヒューリスティック」な判断が必ずしも正しいとは限らないことも、読者はよくご存知のはずである。初対面では信用できると思った人が、実はそうではないことがあるだろうし、その逆もよく起こりうる現象だからである。

 「代表的ヒューリスティック」とは、あるカテゴリーの中から「代表的」な要素を見つけ出し、そこから「ヒューリスティック」に判断する考え方を意味する。
　リンダの紹介文を読んで、リンダの人格を「代表」する特徴として「社会における正義」や「女性差別の問題を追究」というイメージを抱いた読者は、現在のリンダが「フェミニスト活動家」であることに相応しいという「直感」を抱くようになる。
　つまり、論理的思考よりも「代表的ヒューリスティック」を優先させた結果、論理的には間違っているBを選んでしまうわけである。

　ちなみに、初対面の相手があまりアイコンタクトを取らないと、その相手は信用できないというイメージを抱く読者がいるかもしれない。しかし、この種の「非言語コミュニケーション」には、生まれ育った文化圏の影響が大きいことを事前に理解しておくべきだろう。
　欧米の多くの国々では、話している間、基本的にずっと相手の目を見て、聞いている姿勢を示す必要がある。しかしアジア圏では、必ずしもそこまでアイコンタクトを重視する習慣はない。むしろ、タイやシンガポール、ベトナムやラオスなどでは、尊敬する相手や女性の目を直視することがタブーであり、「伏し目がちにする」ことこそが礼儀正しいとみなされている。
　一般にアメリカ人は、初対面の際、比較的アイコンタクトを取らないアジア圏の人々に対して、「裏がありそう」「腹黒い」「何を考えているのかわからない」といった先入観を持つ傾向の強いことが統計的に指摘されているが、これも一種の「代表的ヒューリスティック」といえるだろう。

●選言「PまたはQ」（P∨Q）

　PとQが命題であれば、「PまたはQ」も命題である。論理学では「PまたはQ」をPとQの「選言（disjunction）」と呼び、記号では「P⋁Q」のように表す。この命題は、Pが偽であると同時にQが偽であるときに限って偽であり、それ以外の場合は、真と定義される。

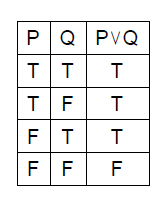
　たとえば、P=「彼は数学科の学生である」、Q＝「彼は哲学科の学生である」であれば、「PまたはQ」は「彼は数学科の学生であるか、または哲学科の学生である」になる。
　この「PまたはQ」という命題は、P=「彼は数学科の学生である」が偽であり、Q＝「彼は哲学科の学生である」も偽である場合に限って偽になる。つまり、彼が数学科の学生ではなく、哲学科の学生でもない場合に限って偽になり、それ以外の場合は真になる。
　つまり、彼は数学科か哲学科か、どちらかの学科の学生であれば、「PまたはQ」は成立することになる。それでは、彼が数学科の学生であり、哲学科の学生でもある場合はどうなるだろうか？

　日本では、数学科は理学部、哲学科は文学部に配置されていることが多いため、その両方に在籍することはできないのが普通である。ところがアメリカの大学では「文理学部（College of Arts and Sciences）」に数学科と哲学科が含まれているため、その両方の学科に在籍することが可能である。実際に、私はアメリカの大学で数学科と哲学科の両学科に在籍し、両専攻（double major）で卒業している。

　というわけで、要するに論理学における「PまたはQ」は、PかQのどちらか一方、あるいは両方が真の場合に真と定義されるのだが、これは日常言語の「または」の意味と必ずしも合致していないことに注意が必要である。

●「ビーフまたはチキンからお選びください」

　読者が国際線の飛行機に乗ってヨーロッパに出掛けるとしよう。機内食の案内に来たキャビン・アテンダントが「お食事は、ビーフまたはチキンからお選びください」と言ったとする。
　論理学における「ビーフまたはチキン」は、どちらか一方を満たしても両方を満たしても「真」である。したがって、読者が「私はビーフとチキンの両方がほしい」と答えたらどうなるだろうか？
　これはキャビン・アテンダントとして就職した卒業生から聞いた話だが、時折、このように「両方」を注文する乗客に遭遇するそうだ。その都度、他の客と公平に扱うため「申し訳ございませんが、どちらか一つをお選びください」と答えることになっているという。ただし、機内食に余りが出た場合には、後で余分の機内食をサービスすることもあるそうだ。

　論理学で用いている「PまたはQ」（P∨Q）を「両立的選言（inclusive disjunction）」と呼ぶ。これはPとQの両方が成立する際にも「真」と判断するからである。
　一方、PとQの両方の成立を「真」と認めずに「偽」と判断する立場の「PまたはQ」（P∨Q）を「排反的選言（exclusive disjunction）」と呼ぶ。
　なお、便宜上「排反的選言」には記号「∨に下線」が用いられるが、これは論理的結合子ではない。

　実は、これは驚くべきことなのだが、論理的には2種類の「または」が存在するにもかかわらず、日常言語では日本語でも英語でも「常識的」にそれらを区別して使っているのである！

　レストランで、ウエイトレスに「コーヒーまたは紅茶をどうぞ」と言われたら、それは「排反的」にどちらか一つを選ぶというのが常識である。
　ところが、同じウエイトレスが「砂糖またはミルクをどうぞ」と言えば、その場合は「両立的」である。なぜなら、砂糖とミルクの両方をコーヒーに入れる客も普通に存在するからである。
　仮に誰かが「PまたはQと交際する」と言えば、常識的には排反的にどちらか一人と交際するという意味を指すが、中には二股をかけて「両立的」に交際を成立させる人がいるかもしれない。この場合の「または」は、「両立的」か「排反的」か、文脈によって異なってくる。

●「排反的選言」を論理的結合子で表すにはどうすればよいか？

　さて、ここで読者には、「排反的選言」を「￢」と「∧」と「∨」の3つの論理的結合子だけで表わしてほしい。

　まず「排反的選言」で大事なことは、PかつQが成立する事態を避けることである。したがって、「（PかつQ）ではない」つまり「￢（P∧Q）」を成立させなければならない。

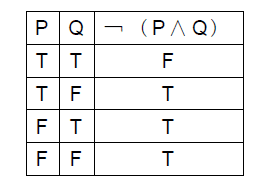
　ちなみに英語では「（PかつQ）ではない」はthat節を用いて「It is not the case that P and Q」のように表現できるので、論理構造が見えやすい。

　ここで「両立的選言」の「（P∨Q）」が成立し、かつ「￢（P∧Q）」も成立すれば、「排反的選言」の出来上がりになる。

　つまり「排反的選言」は、論理的結合子のみを使って表現すると、「（PまたはQ）かつ［（PかつQ）ではない］」（P or Q and it is not the case that P and Q）になる。
　記号が並んで複雑に見えるかもしれないが、この表現によって論理的に厳密に「排反的選言」を表現できることに注意してほしい。

●ド・モルガンの法則

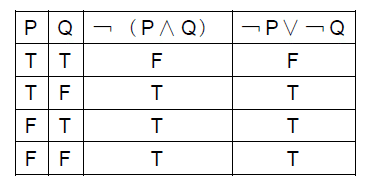
　さて、￢（P∧Q）は￢P∨￢Qと同値である。

　また、￢（P∨Q）は￢P∧￢Qと同値である。

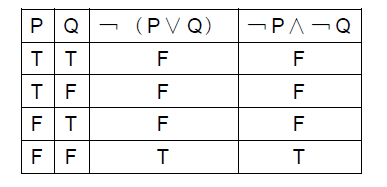
　上記2つは「ド・モルガンの法則」と呼ばれる。読者には、これらの真理表が成立することを、空欄にTかFを記入して、実際に確かめていただきたい。

 「（PかつQ）ではない」（It is not the case that P and Q）は、「Pではないか、またはQではない」（Either not P or not Q）と同値である。
 「（PまたはQ）ではない」（It is not the case that P or Q）は、「Pではなく、かつQでもない」（Neither P nor Q）と同値である。

　ここで「同値」というのは、PとQのすべての組み合わせに対して、まったく同じ真理表が成立することを意味する。

　「ド・モルガンの法則」は、「否定」と「連言」と「選言」の組み合わせで生じる誤読や誤解を避けるために有用なので、その論理構造を覚えておくと、大いに役立つはずである。

●ロジカルコミュニケーションの第5歩は「かつ」と「または」に注意すること！［第1歩～第4歩は、本連載第1回～第4回参照］ 

日常言語では曖昧になりがちな「～でない（否定）」と「かつ（連言）」と「または（選言）」の組み合わせが、論理的結合子を用いると論理的に厳密に表現できることをご理解いただけたと思う。
「記号は苦手」とおっしゃる読者もいるかもしれないが、算数の「＋」や「×」記号が日常生活で役立つように、落ち着いて理解すれば、論理的結合子も非常に有用なので、ぜひ活用していただきたい。 

参考文献
高橋昌一郎（著）『東大生の論理』筑摩書房（ちくま新書）、2010年
高橋昌一郎（監修・著）／山﨑紗紀子（著）『楽しみながら身につく論理的思考』ニュートンプレス、2022年
スマリヤン（著）／高橋昌一郎（監訳）／川辺治之（訳）『記号論理学』丸善、2013年

 イラスト・題字：平尾直子

第4回に戻る

高橋昌一郎（たかはし・しょういちろう）
國學院大學教授・情報文化研究所所長
専門は論理学・科学哲学。主要著書に『理性の限界』『知性の限界』『感性の限界』『フォン・ノイマンの哲学』『ゲーデルの哲学』（以上、講談社現代新書）、『20世紀論争史』『自己分析論』『反オカルト論』（以上、光文社新書）、『愛の論理学』（角川新書）、『東大生の論理』（ちくま新書）、『小林秀雄の哲学』（朝日新書）、『実践・哲学ディベート』（NHK出版新書）、『哲学ディベート』(NHKブックス)、『ノイマン・ゲーデル・チューリング』（筑摩選書）、『科学哲学のすすめ』（丸善）など多数。 

動画【ロジ研#4】ロジカルコミュニケーション入門【第4回】のご案内
本連載の内容について情報文化研究所の研究員たちがディスカッションしています。ぜひご視聴ください！

関連書籍

※「本がひらく」公式Twitterでは更新情報などを随時発信しています。ぜひこちらもチェックしてみてください！