
数学は複雑化する世界を生きぬくための必須のツール。数学による人生の指南書『公式より大切な「数学」の話をしよう』より〔後編〕
数学は自分と無関係と思っていませんか? 実際にはルート検索やSNS、世論調査、医療現場にいたるまで、数学がなければ社会も生活も成り立ちません。8月28日発売の『公式より大切な「数学」の話をしよう』(ステファン・ボイスマン、塩﨑香織・訳)では、20歳でストックホルム大学最年少博士号を取得した若き天才数学者が、身近な事例をもとに数学を通して社会や世の中のしくみへの理解を深める方法を解説。難しい公式や数式を使わなくても簡単にわかり、人生を豊かにする数学の力について語りつくします。
当記事では本書より一部を抜粋・編集し、前編・後編の2回にわたってご紹介します。
*前編はこちらからお読みになれます。
ホームズと数学の共通点
名探偵シャーロック・ホームズは、ロンドンのベーカー街221Bに住んでいた。この住所は実在するが、実際にホームズがその建物で暮らしていたわけではない。架空の人物なのだから、あたりまえだ。ホームズは小説だけでなく、多くの映画やドラマにも登場する。そのため「シャーロック・ホームズがロンドンに住んでいた」と聞かされても、ばかばかしいとは思わない。物語のなかで彼はたしかにそこに住んでいるが、現実のロンドンでは、その名前でその住所に住んだ人物はいない、ということだ。数学についても同じような考え方ができる。
数学は、1つの物語を語るものだ。数や図形をはじめいろいろなものが登場し、プラトンが想像したような世界が描かれる。つまり、どんなものも変化せず、すべてが完璧な論理の体系に沿ってまとめられている世界だ。ところが、永遠不変の数学的実体の存在を否定する唯名論者たちに言わせれば、そのような数学の世界はシャーロック・ホームズの物語と同じく、虚構にすぎない。数学がその物語に登場させるものの世界は実在しないのである。数学者は「数」や「三角形」について語るというが、そんなものは存在していない。現実にあるのは目に見える周囲のものだけ。「数」の普遍概念がふわふわと空に浮かんでいる別世界などないというわけだ。
べつの言い方をしよう。プラトンによれば、数学は人間によって発見される。しかし、数学はすべて人間によって発明されたものであるかもしれない。この考えを進めると、数学は人間が頭の中で創り出したものである以上、数や三角形その他について真であることも「ない」、とおかしなことになってしまう。「3は素数である」「1+1=2」と言うことはできるが、これは正しくない。そもそも数が存在しないのだから「1+1=2」は偽である、というわけだ。「シャーロック・ホームズはロンドンに住んでいた」という命題が、彼は実在しないため偽であるというのと同じように。
それなら、数学は何から何までむだだと、学校で先生に向かって言えないのはなぜか。それは、数学にも(たとえ唯名論的な立場をとっていたとしても)たしかに真だと認められる部分があるからだ。
たとえば、シャーロック・ホームズについての記述は、アーサー・コナン・ドイル卿が書いた物語と一致しているという意味で真実だと言える。仮に僕が「ホームズはアラスカに住んでいた」と主張したなら、作品の描写を示して、それがまちがいであると指摘できるだろう。このように、シャーロック・ホームズについての命題は、すべて作品に基づいて真偽を確かめることができる。数学もしかり。「1+1=3」という主張は、数学の物語とは一致しないのだ。
しかし、ホームズが登場する本の内容を真に受ける人はいないのに、数学者は数学の物語をそのまま受け止める。ここが数学のしくみを説明するうえで微妙なところだ。実際には真実でないことを主張しながら、きわめて厳密かつ有用な学問の体系を構築することがなぜ可能なのか。唯名論者たちはこの問いにまだ満足な答えを得ていない。
哲学的な話は、ここまでにしておこう。哲学者たちの込み入った議論について腑に落ちないところがあってもかまわない。ここで示したかったのは、数学については2つの見方があるということだ。プラトン主義者と唯名論者の主張はたしかに大きく異なっているが、いずれの立場も数学のしくみ、もっと言うなら、人間が数学に取り組むと何が起こるかを説明しようとしている。
プラトン主義者によれば、そのとき人間は抽象的な事物で成り立つ世界についてあらゆる発見をするのだという。一方で唯名論者は、そんな世界は存在せず、すべて人間が発明していると主張する。この2つの考え方をはっきり区別でき、どちらが正しいのか決着がついていないことを知っていれば十分だ。
「おおざっぱなちがい」を理解する
人間は、成長するにつれて小さな差を認識できるようになる。たとえば生後3か月くらいになると、4個の点と6個の点のちがいを区別できる。大人になると、13個の点は12個より多いことも見分けられるようになる。あくまで一般論で、いつもかならず正解するわけではないが、少なくとも2回に1回は多いほうを当てることができる。とはいえ、20個と21個のちがいを数えずに見分けるのは、ほぼ無理と言っていいだろう。だから結局は数えるほうがよい、ということになる。
2004年に行われた実験では、赤ちゃんは大きな数も計算できるという結論が出た。だが、その後明らかになったところでは、赤ちゃんは5+5=5にはおどろくが、5+5=9に対してはべつにおどろかない。反応は5+5=10と同じで、期待していたこととちがうとは認識しなかった。つまり9と10のちがいは区別できていない。この実験で赤ちゃんがおどろいたのは、人形の数が5よりも多いと期待していたのに、見せられたのが5つだけだったからで、計算して10だと思っていたのではない。赤ちゃんの期待はもっとおおざっぱで、「5よりは多いが、ものすごく多くもない数」という程度なのだ。
この「おおざっぱな期待」はどうやって生まれるのだろう。数量のちがいを区別できる脳のはたらきとはどんなものか。これについてはまだ見解が分かれている。僕の考えを述べるまえに、ものや時間の長さに関係する人間の脳の領域について説明しよう。
ものの長さは、見ただけで正確にとらえられるものではない。もちろん、この長さはあの長さの2倍だといったことはすぐ認識できる。長方形のテーブルを目にしたとき縦横の長さがちがうのはわかっても、正確に何センチメートルかまではわからない。時間の長さについてもまったく同じで、10秒と5分のちがいは確実にわかるし、1時間と2時間の差にも気がつく。だが1時間と1時間+1分なら、はっきり区別できはしないだろう。
この認識のしかたは、じつは数量のちがいを認識するしくみにそっくりなのだ。赤ちゃんは、生まれたときからものの長さのちがいを見分けられるし、2種類の音のうち、どちらがより長く続くかも聞き分けられる。人間は成長するにつれて、ものや時間の長さをうまく認識できるようになり、区別できるちがいが増えていく。それでも、正確な値は測ってみなければわからない。
ものを数えない少数民族がたよりにしている目測の能力は、じつはだれもが生まれつき持っているが、成長するにしたがって磨きがかかっていく。この能力は人間だけにあるものではない。サルはもちろん、ネズミと金魚も数量や長さのちがいを認識できるし、このような処理を行う領域は、ほとんどの動物の脳にもあることがわかっている。では、数学についてまったく知識のない動物(人間ふくむ)が数量を把握できるのは、何によるのだろう。
僕はいまのところ、こう考えている。人間が、「おおざっぱなちがい」を認識できるのは、ものや時間の長さの情報をもとに、脳が数量について判断をくだすからだ。何個あるかよりも、どちらが長いかのほうが一目でとらえやすい。長さや面積その他、見分けられる対象を手がかりに、脳はより抽象的な対象、つまり数量を処理している。なお、僕の考えの根拠には、脳はだまされやすいということがある。
わかりやすい例をあげよう。次の図を一瞬だけ見て、数えたりせずに黒い点が多い円を選んでほしい。
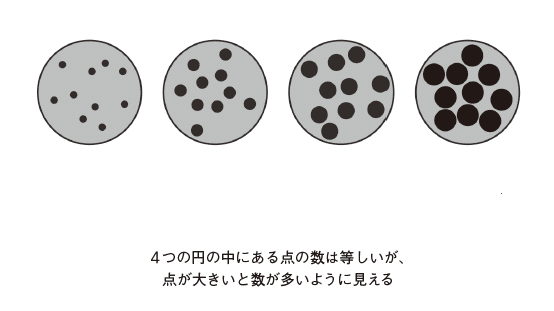
ほとんどの人はいちばん右の円を選ぶのではないだろうか(僕もそうだ)。ほかの円に比べてずいぶんとすき間が少ない、ということは点が多いと思うわけだ。ところが実際に数えてみるとわかるが、どの円でも黒い点の数は同じである。
人間の脳が犯すまちがいはほかにもある。たとえば2つの数を比較するときには、その位置関係、並び方が重要になる。数が「正しく」並んでいれば、その大小の判断がしやすい。小さい数は左側に、大きい数なら右側にある「はず」――脳はそう考える。だから、「9は5より大きいか」という問題で、9が5の右側に並んでいれば、早く答えが出せる。9が5の左にあるときと右にあるときの反応時間の差は自分ではわからなくても、計測値に表れる。「9は15より大きいか」は、15が9の右側にあるほうが答えやすい。
ようするに、脳は見たものに数をリンクさせている。脳が数量を処理するうえで、位置が持つ意味は大きい。これは9や15のようにはっきりした数(字)にかぎらず、点であっても同じだ。しかも、これは人間だけの能力ではない。「大きな数は右側」と考える傾向は、ヒヨコにも見られる。この場合「点が多いものは右側」となるが、こんなふうに数がわかるのは、ヒヨコがものの長さを把握できるからかもしれない。
微積分で速度を出す
変化の速度の計算は、さまざまな場面で行われている。クルーズコントロールではアクセルの制御が計算され、自動運転では軌道修正の範囲も計算される。エスプレッソ1杯分の水を適温に沸かすためにヒーターの設定温度が計算されるコーヒーメーカーもある。また病院でも、たとえば腫瘍が大きくなるスピードを割り出すときにこの計算が使われる。
どんな場合でも、変化に注目するわけだ。「何の」変化かはあまり関係ない。必要な数学は同じだからだ。ここではなるべく単純な例で説明してみよう。たとえば、スピード違反の取り締まり。このとき、走行する車の速度はどうすればわかるのだろう。
いちばん簡単なのは、一定の区間を設定して速度を求めることだ。必要な警察官は2人。1人は測定区間の起点に立って車両が通過した時刻を記録し、もう1人は1キロ先の地点で同じように車両が通過した時刻を記録する。そしてこの2つの時刻から、車両が区間の起点を通過したときの速度を出すわけだが、そのためには車両がその区間の走行に要した時間も計算する必要がある。車両が時速120キロで起点を通過したとすると、区間を走行するには30秒かかる。つまり区間の起点と終点の通過時刻の差が30秒であれば、その車両は時速120キロで走行していたことになる。
本当にそうだろうか。この方法だと、制限速度が時速120キロのところを140キロで走っていたドライバーは、起点で140キロでも、区間の1キロを30秒かけて走り、終点を100キロで通過すれば、計算上の起点の時速は120キロになってしまう。
このような事態を防ぎ、スピード違反を取り締まるには、通過時刻を記録する区間を短くすればよい。半分の0.5キロになれば、時速120キロで走行中のドライバーが減速する時間は15秒しかない。このようにして区間距離を短くしていけば、起点通過速度の計算精度は上がっていく。実際には、ミリ秒(1000分の1秒)の単位で自動車の速度が大きく変化することはないので、区間距離を短くするにも限界はある。道路沿いに設置されている速度表示板はかなり正確だが、それはこの計算を1メートル程度のごく短い距離で行っているからだ。
では、車両が区間の起点を通過するときの正確な速度を知りたい場合はどうだろう。速度表示板の計算で生じるわずかな誤差でさえ許されないとしたらどうするか。計算の精度をさらに上げるには、距離をもっと短くする必要がある。ここまで来れば、「無限」の概念も近い。区間を無限に小さくすることで、無限に精度を上げられる、つまり正確な結果が得られるというわけだ。

プロフィール
ステファン・ボイスマン Stefan Buijsman
1995年、オランダ、ライデン生まれ。15歳でライデン大学に入学し、天文学、コンピュータサイエンス、哲学を学ぶ。18歳で修士号を取得。その後、スウェーデン、ストックホルム大学で通常4年の課程を18か月で修了、20歳でストックホルム大学最年少博士号を取得。現在はストックホルムの研究機関で数学の哲学の特別研究員(PD)。2018年、数学がテーマの児童書(共著)を刊行。同年に刊行された本書『公式より大切な「数学」の話をしよう』は18か国で出版が決定したほか、オランダ文学基金による「2018年注目のノンフィクション10冊」にも選出された。2020年、AIをテーマにした新作を上梓。オランダ、デン・ハーグ在住。

