
「数学」は人生の武器になる! 数学嫌いの中高生や文系の大人も必読。『公式より大切な「数学」の話をしよう』より〔前編〕
数学は自分と無関係と思っていませんか? 実際にはルート検索やSNS、世論調査、医療現場にいたるまで、数学がなければ社会も生活も成り立ちません。8月28日発売の『公式より大切な「数学」の話をしよう』(ステファン・ボイスマン、塩﨑香織・訳)では、20歳でストックホルム大学最年少博士号を取得した若き天才数学者が、身近な事例をもとに数学を通して社会や世の中のしくみへの理解を深める方法を解説。難しい公式や数式を使わなくても簡単にわかり、人生を豊かにする数学の力について語りつくします。
当記事では本書より一部を抜粋・編集し、前編・後編の2回にわたってご紹介します。
数学は何の役に立つのか
高校時代の数学の授業風景が思い浮かぶ。先生をぼんやり眺める僕。電子黒板にはたくさんの数式と、何本かの接線を持つ山型のグラフ。高校で数学を選択した人ならだれでもそうだろうが、公式やグラフの使い方は丸暗記するしかなかった。あのころの僕は天文学科志望で、それが自分のせっかちな性格に向かないとはまだ知らずにいた。もしわかっていたら、どうしていただろう。いまの僕の仕事では、自分の手で計算する必要はまずないが、もし高校生の自分にそのことがわかっていたら? きっとグーグルに、こう打ち込んだだろう。「数学は何の役に立つのか」
数学は現代の社会で重要な役割を果たしているし、数式の成り立ちを追ってみれば、意外と理解しやすかったりもする。グーグルは独自の手法で情報を選別するが、そこからは良くも悪くも数学が日常生活に及ぼす影響の大きさがうかがえる。
数学は役に立つ。本書で示したいのはこのことだ。あんなにつかみどころのなかった数学と、僕はいまそれなりにうまく付き合っている。その意味では、本書は高校時代の自分に向けて書いたとも言えるが、もともとは、学校を出ればわずらわしい数学の計算など忘れてもこまらないと思っている人(昔の僕もここに入る)を想定して書いていた。現在の僕は数学の哲学者で、数学の成り立ちと、人間が数学をどうやって身につけるかについて考えている。この立場から、仕事で必要かどうかには関係なく、数学の実際的な価値はとても大きいことを理解している。数学は公式だけで片づけられるものではない。だから本書に公式や数式はほとんど登場させなかった。具体的な計算が求められるときに公式は便利だが、それにたよるあまり、ベースとなる考え方の理解がおろそかになってしまうこともよくあるからだ。
数学は、多くの人が思うほど無意味で不可解なものではない。むしろその逆だ。このことを示すために、本書ではいくつかの数学の領域とその背景にある考え方を取りあげる。
Netflixの「マッチ度」
映像をストリーミング配信するNetflixでも、数学が活用されている。作品ごとに緑色で示されている数字は、ふだん見ている作品との「マッチ度」だ。マッチ度が高いので気に入ると思って視聴したのに、まったくおもしろくなかった、ということもたまにある。しかし、この数字をそれなりに信用してマッチ度の高い作品を選んでいくと、好きな映画やドラマの傾向がはっきりしてきてハズレが少なくなるはずだ。マッチ度は、新たな作品を視聴するたびに自動的に更新される。つまりコンピューターのプログラムで、ユーザーの好みに合う作品かどうかを判断しているわけで、作品の良し悪しを評価しているわけではない。
基本的な考え方はとても単純で、「よいオススメ」とは、本人が「見て」気に入っている作品に似たものであるということだ。Netflixでは、世界じゅうの会員が「こちらもオススメ」にあげられた(つまり視聴ずみの作品とのマッチ度が高い)作品を見ている。映画が2作あったとして、片方を見たあとでもう1作を見る人が多ければ、その2作は似ているとみなせる。たとえば〈アイアンマン〉のあとで〈アイアンマン2〉を見た人がとても多いなら、この2本は似ているにちがいないので、〈アイアンマン2〉は〈アイアンマン〉を見た人にとって「よいオススメ」と言える。Netflixを利用する人が多いほど、レコメンド機能の精度も上がる。コンピューターで、特定のユーザーと視聴履歴の似ている人がすでに見た作品を選び出せるからだ。
映画1本、ドラマ1作品をそれぞれ1個の円で示すとする。そのような図を使って計算を進めるには、円と円を結ぶ線ごとに数値が明らかでなければならない。ここでの数値は、クリックした作品を両方とも見た人の数だ。3作の映画だとすると、次の図のようになる。
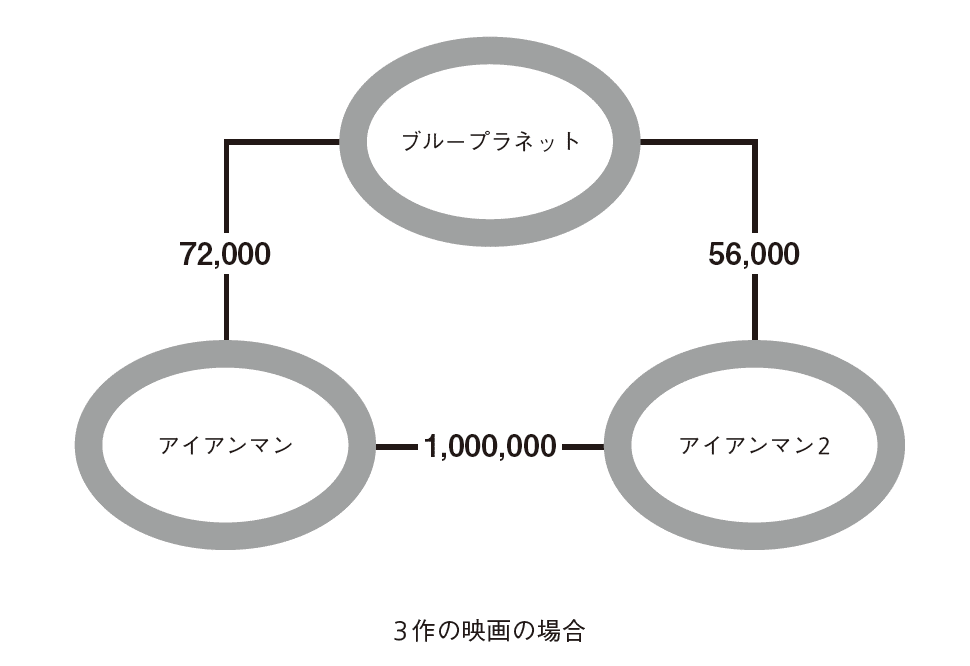
この図から、ユーザーの好みと各作品のマッチ度がどうなるかを考えてみよう。あるユーザーがNetflixで〈アイアンマン〉だけを見ていたとする。そのときコンピューターの仕事は、このユーザーが〈アイアンマン2〉と〈ブループラネット〉をどの程度気に入るかを予想することだ。図の数字からすると、〈アイアンマン2〉のマッチ度は相当高くなる。好みが同じユーザーの多くが見ている作品であれば、「よいオススメ」、つまり気に入る可能性が高い。
反対に〈ブループラネット〉のスコアは低くなる。これは、〈ブループラネット〉と〈アイアンマン〉の両方を見た人がずっと少ないためだ。〈アイアンマン2〉と〈ブループラネット〉の両方を見た人はさらに少ない。この結果、〈ブループラネット〉のマッチ度は低くなる。こうして「こちらもオススメ」には〈アイアンマン2〉が表示される。コンピューターはさらに、この計算結果(たとえばあるユーザーが〈アイアンマン2〉をどのくらい気に入るか)をべつの作品に関するマッチ度の正確性を高めるために活用する。
数学がなければ暮らせない
僕たちは毎日、いろいろな場面で数学に接している。もちろん、文字どおりの意味ではない。数学について考えるのが仕事の僕でも、ふだんは計算などしなくてもやっていける。だが、その一方、人目にふれないところで数学が重要な役割を果たしていることは、あまり知られていない。数学にたよらなければグーグルマップのルート検索はありえないし、Netflixのレコメンド機能も、かなりあやしいものになるだろう。グーグルの検索エンジンも使いものにならないはずだ。
Netflixやグーグルで活用されているのは、いずれもグラフ理論と呼ばれる数学の一分野だ。ただし、生活にかかわる数学のなかで重要なのはこれだけではない。たとえば、具体的な数値をふくんだニュース記事には統計が使われていることが多い。選挙前の世論調査を伝える記事はよくあるが、得られた数値から国全体の政治傾向がわかったと言われても、それをどう解釈するか。この手の調査はまずあてにならない。最たる例は2016年のアメリカ大統領選挙だ。世論調査によればヒラリー・クリントンが圧勝すると言われていたが、そうはならなかった。つまり、数値からは誤解が生まれやすいのだ。
事実を曲げる意図はなかったとしても、結果的にうそになってしまうこともある。この種の統計にはさまざまな事実が隠れているので、数値をあつかうときにどんなまちがいが起こりうるかをわかっていないと、さも大ごとのように伝えられる記事の内容をうのみにしてしまう恐れがある。世論調査を読みとくのはいいが、その解釈がまったく見当ちがいかもしれないとしたら、そんな記事はどこまで信頼できるものだろうか。
あるいは、政府がある制度に関する方針を変更したというニュースを目にしたとする。改編は賢明な判断だろうか。ここで客観性を第一に考えるなら、新制度の影響試算に目を通すべきだろう。どの国にも、経済政策や財政状況を調査・分析する機関があるはずだ。ある政策の影響を判断するといっても、考慮すべき点はいくつもあり、その全部を見通すことは不可能に近い。たとえばある試算で「長期的に可処分所得は増加傾向」と示されたとき、それはあらゆる要素をわかりやすい一点に集約して表現しているにすぎない。そこにいたるまでにはたくさんの数学が使われている。
もう少し身近な話をすれば、エスプレッソをいれるときにも数学は使われている。高機能なエスプレッソマシンなら、お湯を沸かしてコーヒーを抽出するだけでも相当の手間がかかる。まず確認されるのは水が温まる速さ。そしてこれをもとに、加熱を続けるか、少し冷めるのを待つかを判断する。理想の温度になるまではこの繰り返しだ。考えてみたことすらないかもしれないが、エスプレッソ1杯にも、高校時代に習った数学の公式が使われているのだ。
こう見てくると、数学が生活に及ぼす影響はかなり大きい。自分で計算することはないにしろ、僕たちは毎日さまざまな計算の世話になっている。判断の際に参照する情報も、なんらかの数学的な処理の結果だと言ってかまわないだろう。グーグルやフェイスブックなど、情報をフィルタリングして表示するウェブサイトでは、コンピューターによる計算に基づいて検索結果を表示しているからだ。身のまわりにあるテクノロジーにも、数学を利用したものが増えてきた。全自動のエスプレッソマシン、飛行機の自動操縦、仕事に欠かせないパソコン。これらはすべて数学がベースになっている。さまざまなところで数学が使われるようになるなかで、数学とその影響をある程度理解しておくことがますます大切になっているのだ。数学の知識が多少ともあれば、現代社会でどれほど役に立つだろう。
後編(8月27日公開予定)へ続く

プロフィール
ステファン・ボイスマン Stefan Buijsman
1995年、オランダ、ライデン生まれ。15歳でライデン大学に入学し、天文学、コンピュータサイエンス、哲学を学ぶ。18歳で修士号を取得。その後、スウェーデン、ストックホルム大学で通常4年の課程を18か月で修了、20歳でストックホルム大学最年少博士号を取得。現在はストックホルムの研究機関で数学の哲学の特別研究員(PD)。2018年、数学がテーマの児童書(共著)を刊行。同年に刊行された本書『公式より大切な「数学」の話をしよう』は18か国で出版が決定したほか、オランダ文学基金による「2018年注目のノンフィクション10冊」にも選出された。2020年、AIをテーマにした新作を上梓。オランダ、デン・ハーグ在住。

