
「思考入門 “よく考える” ための教室」第6回 〔ヒトの脳は論理的思考には向いていない。ならばどうする!?〕 戸田山和久(文と絵)
早いもので今年も師走になっちゃいました。おとなにとってはあわただしい月。でも、みなさんはもういくつ寝るとメリークリスマスに冬休みにお正月! お楽しみですねえ。でも、勉強もしっかりやりましょうね。はい、「思考入門」も6回目、いよいよ第2部に入りますよ。ここまでの連載をしっかり読んだみなさんは、「論理的」ってどういうことか、バッチリ理解できましたね。戸田山さん、6回目で星一徹ですよ。ちゃぶ台ひっくり返しますよ。なんせ、わたしたちのアタマって、もともと論理的思考には向いてないって言うんですから。困りましたねえ~~。でも戸田山さん、どうすればいいかもキッチリ教えてくれます。いやあ、哲学ってホントにすんばらしいですねえ。それでは、じっくり読んでくださいね。
AランチかBランチかそれが問題だ
さて、『思考入門』も今回で第6回、いよいよ佳境〈かきょう〉に入ってきた。ここまでは、論理的によく考える・書く・話すというのはどういうことかを明らかにしてきた。でも、わたしたちの頭はそれほどデキがよくないのね。むしろヒトの脳は論理的思考にあまり向いていないと言ったほうがよいくらいだ。それじゃあ、どうしたらよいのだろう。『思考入門』後半戦のテーマはこれだ。
まずは、わたしたちはそんなに論理的思考が得意ではないという事実に気づいてもらおう。気づいたら、なぜそうなのかを考えよう。そのうえで、どうすればよいのかを考えよう。
というわけで、こんな例から始めてみよう。キミの学校は学生食堂があって、2種類の日替わりランチを出してくれる。AランチとBランチだ。値段は同じ。どっちも同じくらい美味〈おい〉しい。しかもキミは好き嫌いの全くないよい子ちゃんだ。だから、いつもどっちのランチを頼むかで迷ってしまう。決め手がないから、もう悩むこと悩むこと。チケットの販売機の前でずっと決めかねていると、後ろに並んでいる友だちから「早く決めてくれよ。イライラ」と言われる。すみません。
そこでキミは、毎朝ウチを出る前に、その日のランチをどっちにするか、百円玉を投げて決めておくことにした。表が出たらAランチ。裏が出たらBランチ。これで問題解決。で、今日は木曜日だ。今週はここまで、月曜日に表、火曜日に表、水曜日には表と、3回連続で表が出ている。そこでキミはこう考えた。今日も表が出そうだぞ。
でも、これは間違いなんだ。前の日に表と裏のどっちが出たかは、次の日にどっちが出るかに関係ない。いつも、表が出るか裏が出るかは五分五分だ。だから、今日も、表のほうがより出やすいということはない。あくまで五分五分。わかりにくかったら、キミは毎日違う百円玉を投げると考えてみたらよい。昨日投げた百円玉は、今日投げる百円玉と何の関係もないことがはっきりするだろう。
2つのダメ推論
この間違いをもうちょいちゃんと分析してみよう。証拠と主張とサポート関係という論理的思考のパターンに当てはめてみると、キミは次のような推論をしたことになる。
月曜日には表が出た
火曜日には表が出た
水曜日には表が出た
したがって、木曜日にも表が出るだろう
でも、これってよい論理的推論ではない。月曜日から水曜日までにどちらが出たかは、木曜日にどっちが出るかと何の関係もないので、3つの「証拠」は結論をちっともサポートしていない。これは有名な間違いなので、「ギャンブラーの誤謬〈ごびゅう〉」という名前がついている。
この逆の間違いもある。木曜日のコイン投げの結果も表だったとしよう。4回連続で表が出たというわけだ。キミの「木曜日にも表が出る」という予想は見事に当たったことになる。ここでぜったいに言っておかねばならないのは、結果として当たっていたから、キミの行った推論は成功だった、よい論理的推論だったということにはならない、ということだ。キミの推論はサポート関係が成り立っていないのでダメな推論だった。でも、まぐれで結論が当たった、というのがほんとうのところだ。
さて、今週は月曜日から木曜日までずっと表が出続けている。で、金曜の朝にキミはこう考えた。そろそろ裏が出てもいいんじゃないか。今日は裏が出そうだぞ。この推論のどこがダメか、もう分かっているね。
月曜日には表が出た
火曜日には表が出た
水曜日には表が出た
木曜日には表が出た
したがって、金曜日には裏が出るだろう
4つの「証拠」は、主張が成り立つか(成り立ちやすいか)に何の関係もない。だから、相変わらず主張はサポートされていない。
でも、ゲームをやっているときとか、ついこのように考えてしまわないか?ずっとダイヤが出ているのはおかしいから、そろそろクラブやハートが出るんじゃないかって。これも有名な間違いで「逆ギャンブラーの誤謬」という。表、裏、どっちの結論を出しても間違った推論なんだね。でも、わたしたちはついそういうふうに考えてしまう。
「珍しいことが起きたぞ」と「よくあることが起きたぞ」
もうちょっとランチの事例を続けてみよう。コイントスを始めて2週間がたった。第1週は、表表表表表だった。第2週は、表表裏表裏となった。2週目の終わりに、キミが次のように思ったとしよう。1週目は5回連続「表」なんてずいぶん珍しいことが起きたけど、2週目はよくある結果に落ち着いたな。
ブーッ。間違い警報発令。「よくある結果に落ち着いた」というのを、「表表表表表より表表裏表裏という並び方のほうが起こりやすい」という意味で使っているなら、キミは間違っているぞ。
すでに言ったことの繰り返しになるけど、前の日に表裏のどちらが出たかは、次の日にどちらが出るかと関係ない。前の日のコインが、次の日のコインに「オレ、表を出しといたからさ、キミも表にしときなよ」などと言ったりはしないよね。どの日も、表が出るか裏が出るかは五分五分(これを確率2分の1、という)。だったら、表表表表表と5回連続で表が出るのは、「前に何が起きたかにかかわらず確率2分の1で起こることがら」が5回起きたので、2分の1を5回かけて32分の1の起こりやすさで起こる。じゃあ、表表裏表裏はどうか。これも、前に起きたことによらず確率2分の1で起こることがらが5回起きている。なので、やっぱり32分の1。どっちも起こりやすさは同じなのだ。
でも、何だか表表裏表裏のほうが「ありそう」に思えてしまう。なぜだろう。5回百円玉を投げて表裏がどういう順序で出るかをぜんぶ書き出してみよう。
(a)表表表表表
(b)表表表表裏 表表表裏表 表表裏表表 表裏表表表 裏表表表表
(c)表表表裏裏 表表裏表裏 表裏表表裏 裏表表表裏 表表裏裏表
表裏表裏表 裏表表裏表 表裏裏表表 裏表裏表表 裏裏表表表
(d)裏裏裏表表 裏裏表裏表 裏表裏裏表 表裏裏裏表 裏裏表表裏
裏表裏表裏 表裏裏表裏 裏表表裏裏 表裏表裏裏 表表裏裏裏
(e)裏裏裏裏表 裏裏裏表裏 裏裏表裏裏 裏表裏裏裏 表裏裏裏裏
(f)裏裏裏裏裏
目がチカチカしてきたぞ。数えてみるとぜんぶで32通りある。このひとつずつは同じ起こりやすさで起こる。だから、表表表表表も表表裏表裏も起こりやすさは32分の1。ここまではいいね。
なのに、表表裏表裏のほうが表表表表表より「ありそう」に思えるのは、表表裏表裏は、「3回表、2回裏」のグループ(c)ぜんたいを代表しているからだ。(c)グループは10通りある。だから「3回の表と2回の裏が混ざって出る」というのは表表表表表の10倍起こりやすい。そして、表表裏表裏は「3回の表と2回の裏が混ざって出る」の代表とみなされているんだ。もしかりに、表表裏表裏が「表と裏が混ざって出る」の代表だとするなら、もっとたくさんを代表している((b)~(e)の30通りを代表している)。
いずれにせよ、わたしたちは、表表裏表裏をそれじたいとして理解するのではなく、それと似たたくさんのケースの代表として見てしまう。だから、表表裏表裏の起こりやすさを正しく評価することができなくなって、「いかにも起こりやすい」「ありそう」だと思ってしまう。
わたしたちは「あるある」にヨワい
わたしたちは典型例の代表だとみなしたものを、実際以上に起こりやすいと判断するようにできているらしい。これと似たしくみで生じてしまう判断ミスの例をもうひとつあげてみよう。次の問題を考えてみてほしい。
Aさんは最近タピオカドリンクにはまっている。特にお気に入りなのは、抹茶ミルクにタピオカを入れたものだ。友だちと連れ立ってあちこちのお店に出かけて飲み比べをしている。いつか、本場の台湾に女子旅に出かけたいと思っている。10月の31日はハロウィンの仮装をして渋谷に出かけた。夜遅くまで楽しんでいたら、両親に叱〈しか〉られてしまった。
さて、Aさんは次のどちらである可能性のほうが大きいだろうか。
(1)Aさんは都内の女子高生である。
(2)Aさんは流行に敏感な都内の女子高生である。
(2)と答えてしまったキミ! 間違っとるよ。都内の女子高生のうち、流行に敏感なのはその一部だ。都内の女子高生の中には、流行に敏感な人とそうでない人がいる。だから、「都内の女子高生である」可能性のほうが、「都内の女子高生でしかも流行に敏感である」可能性よりも大きいはずだ。
でも、多くの人が(2)と答えてしまう。それは、タピオカだの女子旅だのハロウィンが好きという情報に、「流行に敏感な女子高生」というAさん像が、よりピッタンコだからである。「いかにもあるある」だ。なので、わたしたちは(2)の可能性を大きめに評価してしまう。

ことがらそのものではなく、典型例の代表として見てしまう傾向がわたしたちには備わっている。そのため、起こりやすさや可能性の判断を誤ってしまう、というわけだ。
最初の数字があとあとまで尾をひく
わたしたちにもともと備わっている判断傾向のせいで生じる間違いの具体例をあげだすとキリがない。もう少しあげておこう。今度のは、トゥベルスキーとカーネマンという超有名な心理学者の実験だ。
国連の加盟国のうちアフリカの国は何パーセントくらいを占めると思いますか、と実験に参加してくれた人たちに尋ねる。正確に知っている人はほとんどいないので、みんな当てずっぽうで答えることになる。このとき、ルーレットを回して、出た数字をみんなに伝えて、それよりどのくらい大きい(小さい)と思いますか、という聞き方をする。ルーレットで出た数字が10だったグループの場合、みんなの答えの平均は約25パーセントになった。一方、ルーレットの数字が65のグループでは答えの平均は約45パーセントだったそうだ。
これって、おかしいでしょ。だって、ルーレットの数字は、答えを求められている数字と何の関係もない。そして何の関係もないとみんなもわかっている。なのに、その関係ない数字に判断がひっぱられてしまったのである。どうやら、わたしたちは、何かを見積もるのに、最初に与えられた数字を出発点にして、それに調整を加えることで答えを見つけようとする傾向があるみたいだ。でも、たいていの場合、その調整は十分に行われず、最終判断が最初の数字に影響されてしまう。
飛行機と自動車とどっちがアブナイ?
飛行機と自動車とどっちが危険な乗り物だろう。なんとなく飛行機のほうがアブナイから怖いと思っている人は多いだろう。わたしも飛行機は好きじゃない。できるかぎり陸路で行きたいと思っている。それに、やっぱり乗っていて怖いのは飛行機だ。とくに、突然ガクンと機体が落っこちて、からだがフワッと浮く感じがするとき、コワイなあ。
でも、コワイのとアブナイのとは違う。怖いと思うのはわたしの勝手だが、危ないかどうかはもっと客観的に決まっているはずのことがらだ。そこで、どっちがより危険なのか数字で調べてみよう。交通機関の「危なさ」を測るにはどういう数字を使ったらいいだろう。真っ先に思いつくのは事故で亡くなった方の数だ。2018年に飛行機事故で命を落とした人の数は世界中で556人。自動車事故の死亡者数は日本だけで3532人(これでも統計を取り始めた1948年以降で最も少ないんだそうだ)、世界全体では約135万人。圧倒的に自動車事故のほうが多いね。
そうか、自動車のほうが飛行機の何千倍も危ないんだ、スッゲー自動車って危険、と早とちりしてはイケナイ。だって、自動車に乗る人のほうが飛行機に乗る人よりずっと多いんだから。利用者が多ければ、事故に巻き込まれる人も多くなるよね。というわけで、同じ利用者数あたりの死亡者数を比べないといけない。ちょっと古い数字になるけど、こんなのが見つかった。利用者数100万人あたりの事故による死者数は、自動車が0.027人、飛行機は1.8人。こんどは飛行機のほうが危ないということになったぞ。
でも、これじゃ航空会社は納得しないんじゃないかな。一人の利用者がどのくらいその乗り物に乗っているかを考えに入れていないからだ。飛行機はいったん乗ると、かなり長い間乗り続ける。アメリカやヨーロッパに行く便では10時間以上乗らないといけない。これに対して、そんなに長い間自動車に乗り続ける人は、いるにはいるけど(運転手さん)、それほど多くはない。たいていの人は、通勤や通院、買い物、送り迎えに使ったりしている。「ちょっとそこまで」なのである。あとは、ただ駐車場をふさぐだけ。当の自動車会社じたい、この稼働率の低さは社会のムダだと考えて、一家に一台じゃなくていいんじゃないのと言い出しているくらいだ。
10時間乗り続けて遠くまで行く間に事故にあっちゃった、というのと、近所まで5分乗ってたら事故にあっちゃったというのを一律に扱うのはおかしいんではないの、ということになる。そうすると、乗っていた時間あたり、あるいは移動距離あたりの数字で比較しないといけないような気がしてくる。「利用者数あたり」と「移動時間または距離あたり」のどっちも考えに入れて比べるにはどうしたら良いだろう。
そういうときよく使われるのは、「利用者一人がこれだけの時間(距離)移動する間に、平均してどれくらい死亡事故にあってしまいそうか」だ。具体的には、事故死亡者数を利用者数と一人当たりの平均移動時間(距離)の両方で割り算してあげればよい。
そういう数字として、こういうのを見つけた。一人が1マイル移動する間にどのくらい事故で死にそうかというデータだ。ただし、この数字はすごく小さくなるので、わかりやすいように100億倍してある。それによると、自動車は0.55、飛行機は0.38になる。自動車のほうが危険、という具合に逆転している。
でも、こんどは自動車の味方から反論が出そうだ。ほとんどの飛行機事故は離陸するときと着陸するときに起きている。いちばん長い時間、長い距離を進む水平飛行のときは事故が起きにくい。そうすると、水平飛行の時間・距離(しかもたっぷり)も含まれる移動時間・距離で割り算してしまうと、飛行機のほうの数字が小さくなりすぎるのではないだろうか。「利用者数あたり」のほうが公平に比べているのではないか。
というわけで、「飛行機と自動車とどっちがアブナイ」問題にただひとつの答えはない。客観的数字で議論しましょうね、というのはよいとしても、どのような数字を使って比べるかによって結論は変わってしまう。
なぜ飛行機のほうがアブナイと思っちゃうのか?
わかったことは、自動車に比べて飛行機のほうがずっと危ないと一概〈いちがい〉には言えないということだ。どういう数字を使うかによって「どっちが危ないか」は逆転してしまう。にもかかわらず、わたしたちの多くがなんとなく飛行機のほうが危ないのではないかと思いこんでいる。なぜだろう。
心理学者たちによれば、答えはこうなる。それは、飛行機事故のほうが目立つからだよ。自動車事故はよほどのことでないかぎり報道されない。日本全国で、1日に平均して10人亡くなっているのだ。そりゃいちいち報道しないだろう(それでよし、と言ってるんじゃないからね)。一方、飛行機事故は必ず報道される。めったに起こらないが、いったん起きてしまうといっぺんにたくさんの人が亡くなる。無残に散らばった破片とか、燃え上がる機体の映像を何度も見せられる。センセーショナルに報道される飛行機事故のほうが、言葉は悪いが「劇的」なのである。飛行機は危ないという記憶が残る。そして「事故」と聞いたときに思い出しやすい。
どうやらわたしたちは、目立つ事例、つまり最近起きた、派手に報道され、印象に残りやすく、感情を揺さぶる事例、そのため記憶にとどまりやすく、思い出しやすく想像しやすいような事例を頼りに考えるようにできているらしい。この思考傾向が悪さを働くと、そうした目立つ出来事をじっさい以上に「起こりやすい」と判断してしまうことになる。
さっき出てきたトゥベルスキーとカーネマンはこんな実験をしている。アルファベットの「k」で始まる英単語(kingとかknowとか)と3つめの文字が「k」であるような英単語(inkとかankleとか)のどっちが多いでしょう、と質問する。多くのひとが「k」で始まる単語と答えるが、本当は3つめが「k」のほうが倍近くもある(どうやって勘定したんだろうね)。なぜだろう。そりゃ「k」で始まる単語のほうが思いつきやすいからだ(じっさい、この原稿を書いていて、inkとankleを思いつくのにすごく苦労した)。
仮説を立てて確かめる、というのはいいんだけど……
ここまで、わたしたちの頭は論理的に考えるのがあまり上手ではないかもよ、という例をあげてきた。3種類の例を紹介したけど、これらはみんな「どのくらい起こりやすそうか」についての判断にかかわるものだった。「あるある」な典型例を使って考えたり、思いつきやすい事例を使って考える傾向がわたしたちにはあって、それを自覚しないで判断するとヘンなことになる。
そこで、いきなり判断する(即断する)のはやめましょう、とりあえずそれは仮説としておいて、仮説が正しいかどうか実験や観察や調査をやって確かめましょう、ということになる。けれども、こんどはここに落とし穴がある。仮説を確かめようとするときも、わたしたちには困った傾向があるんだ。
それをわかってもらうために、ちょっとしたゲームをやってみよう。参加した気分になって読んでちょうだい。まず、わたしが3つの数を並べるひとつのルールを心の中に思い浮かべておく。キミの役割は次のような問答を通じてそのルールを当てることだ。
キミは3つの数の列を言う。その列が私の考えたルールに当てはまっているなら、私はイエスと言う。そして、当てはまらなかったらノーと言う。この問答を繰り返して、キミは私の思い浮かべたルールがどんなルールかを推測する。ゲームのやり方はわかったかな。それじゃ、最初にヒントをひとつ出しておこう。「2、4、6」はイエスだ。私の頭の中にあるルールに当てはまっている。次はキミの番だ。どんな質問をするかな。ほんとうはキミたちの一人ひとりとプレイしてみたいところだけど、それは無理なので、よくあるなりゆきを書いておこう。だいたい次のようになるんじゃないかと思う。
キミ: 1、3、5はどうですか?
私: イエス。「1、3、5」は私の頭の中のルールに合っています。どう? ルールは分かった?
キミ: うーん「2ずつ増えていく3つの数」というルールかな。
私: なるほど。ではそれを確かめるために、ほかにどんな数字の列を尋ねればいいかな。
キミ: 3、5、7?
私: イエス。
キミ: じゃ、100、102、104はどうすか?
私: イエス。ここまでの質問で、確実に当てられたと言っていい?
キミ: ええ、ぜったい確実ってことは言えないけど、最初よりずっと自信が出てきました。やっぱり「2ずつ増えていく3つの数」でしょ?
たいていはこんなやりとりになる。キミがあげた数字の列は、どれもルールに当たっている。でも、「2ずつ増えていく3つの数」は正解ではない。私が考えたルールは「3つの数がみんな違う」だったんだもん。なーんだ。
キミは、「2ずつ増えていく3つの数」というルールじゃないかしら、という仮説を立てたわけだ。だから、「1、3、5」「3、5、7」「100、102、104」という例を次々に考えて、自分の仮説が正しいことを確かめようとした。で、そのつど「イエス」という答えをもらって、どんどん確信を深めていった。
けれども、このままだと何時間やってもキミは正解にたどり着けない。キミは「2ずつ増えていく3つの数」という仮説(キミ仮説)を捨てて、あるいは修正して「みんな違う3つの数」という仮説(正解仮説)に取り替えないといけないんだけど、キミ仮説を満たす数の列ばかりを挙げて仮説を確かめようとすると、キミ仮説を満たすものはぜんぶ正解仮説も満たすので、いつも返ってくる答えは「イエス」になっちゃう。だから、キミは自分の仮説が間違いだということにいつまでたっても気がつけない。
キミがするべきことは、自分の仮説に反する例を試してみることだ。たとえば、「1、3、7」と言ってみる。そうすると、私は「イエス」と言う。ここではじめて、「2ずつ増えていく3つの数」じゃないな、と思える。そこで仮説を手直しする。「だんだん増えていく3つの数」とか。これを確かめるときにも、「1、3、9ですか?」とか、そんな質問ばかりしていてはダメだ。あえて仮説に当てはまらない例を訊〈き〉いてみる。「1、9、3」ですか? 答えはまたもやイエスだ。そうするとまた仮説を変えないといけない。という具合にやっていると、やがて正解仮説に達するだろう。
でも、たいていの人は、確かめたい仮説に反する例を思いついて、それで仮説を試してみるということがとっても苦手なんだ。なぜか、自分の仮説に当てはまる例ばかりを探そうとしてしまう。こうしたわたしたちの心の傾向は「確証バイアス」と呼ばれている。
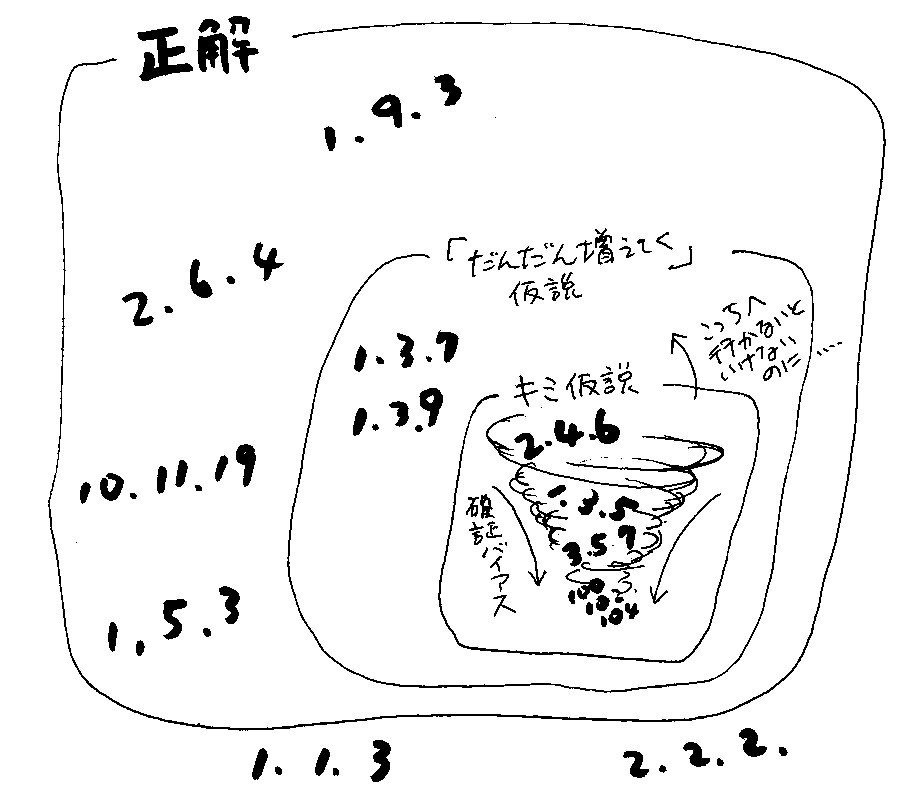
「確証バイアス」に陥ると、正解からどんどん遠ざかってしまう
「心の命ずるままに」やってるとヒドいことになる
こんな具合で、わたしたちの心にはいろいろヘンな癖がある。心理学者はその「癖」を「バイアス」と呼んでいる。もともとは対角線とか斜めの線といった意味だ。ここから、まっすぐから逸〈そ〉れていってしまう「偏〈かたよ〉り」を意味するようになった。
これらのバイアスが組み合わさると、ときとしてすごく困ったことが起こってしまう。たとえば、社会に暮らす少数派(マイノリティー)のひとりが凶悪犯罪を犯したとする。凶悪犯罪じたい珍しいことだが、マイノリティーが犯したとなるともっと珍しい。ニュースにも取り上げられる。多数派の起こした事件はほとんど報道されないのに。というわけで、この事件はいろんな意味で「目立つ」。そうすると、目立つ事例をよく起こることであるかのように捉えてしまう、というバイアスのおかげで、その報道に触れた人は「◯◯人は凶悪なヤツらだ」と思うようになる。
このような考えを抱くようになると、確証バイアスによってその考えが当てはまる例ばかり探すようになる。◯◯人が犯罪を犯したというニュースにばかり注目するようになる。多数派も犯罪を犯すのだが、その情報は無視されるか、忘れられてしまう。こうして、その人の「◯◯人は凶悪だ」という思いは訂正されるどころかどんどん強められてしまう。
こうして生まれてくるのが「偏見」というやつだ。おそらくキミもぜったいになんらかの偏見をもっている。だって、わたしたちの心は偏見を抱いてしまうようにできているんだもん。そして、偏見はわたしたちの社会をひどく生きにくいものにしてしまう。
なぜ心はバイアスをもっているのか
典型例で代表させて考えちゃう、目立つ事例、思いつきやすい事例で考える、仮説に当てはまる例ばかりを探そうとする。なんでわたしたちの心はこんなバイアスをもっているのだろう。答えは、わたしたちの心も進化の産物だから、というものだ。進化の産物だから、ヒトが進化してきたそのときそのときの環境の中で、生きのびるのに都合のよい性質をもつようになっている。心に備わったバイアスは、生存に都合がよいところがあるんだ。だから、いまでも残っているのである。
どういうふうに都合がよいかというと、情報処理をするのにかかるコストを節約するのに都合がいいんだ。ヒトに限らず、生きものは外から取り入れた情報を処理して、状況に応じてうまい行動を選んで生きていく。でも、そのための情報処理には時間とかエネルギーといったコストがかかる。ヒトの脳の重さは体重の2%しかない。でも、とりいれたエネルギーの18%も使っている。さらに、処理しなければならない情報はたくさんある。しかも待ったなし。
森の中からシマシマの巨大なネコみたいな動物が飛び出してきた。「トラかもしれない」と思う。このとき、トラでない可能性もあるからというので、反証例をいろいろ探そうとして、時間とエネルギーを費やす生きものは、うまく生き残れないかもしれない。むしろ、「シマシマだ。ということはトラだ。きゃー逃げろ」という、あまり深く考えない生きもののほうが生き延びやすいかもしれない。

「あまり深く考えない生きもの」のほうが生き延びる!
正確さや厳密さばかりを求めてコストをかけすぎるのは、生き残るうえで有利な戦略とはかぎらない。厳密さや正確さをちょっと犠牲にしても、情報処理コストを節約して、状況に素早く対応したほうがよいときもある。飛び出してきたのが本当はトラでなかったとしても、いいじゃないか。トラかどうか厳密に確かめようとしてぐずぐずしているうちに食われてしまいました、というのよりはるかにマシだ。

情報処理に時間とエネルギーをかけると、どうなる?
典型例で代表させて考えるのも、コストの節約になる。そして、たいていの場合はそれでうまくいく。この世では、典型的なことは同時に「起こりがち」なことでもあるから。思いつきやすい事例で考えるのも、たいていはうまくいく。この世で起こりやすいことは、思い浮かべやすいことでもあるから。
というわけで、生き残るのに都合がよかったからこそ、わたしたちの心にはいろんなバイアスが備わっているんだ。だから、こうしたバイアスを完全になくしてしまうというようなことはできない。根本的な「頭脳改革」は、どだい無理な話だ。
でも、たんに自分が生き延びればいいやというのではなく、この世がほんとうのところどうなっているのかを知りたいよとか、どうせ生きるなら道徳的にも正しく生きたいよと思うようになると、心にもともと備わっているバイアスがジャマになってくる。差別や偏見をなくして、自由で平等な世の中にしたい、と思うと、偏見の原因になっているバイアスが困ったことになってくる。
真理を知るとか、よりよい社会を築くといった目標を実現するには、考えないといけない。でも考えるためにわたしたちがもっている唯一の手段である脳みそがその目標の実現を妨げることがある。こりゃ困ったねえ。どうしたらいいんだろう。次回からはこの問題を考えていこう。
了
プロフィール
戸田山和久(とだやま・かずひさ)
1958年、東京都生まれ。発行部数24万部突破のロングセラー『論文の教室』、入門書の定番中の定番『科学哲学の冒険』などの著書がある、科学哲学専攻の名古屋大学情報学研究科教授。哲学と科学のシームレス化を目指して奮闘努力のかたわら、夜な夜なDVD鑑賞にいそしむ大のホラー映画好き。2014年には『哲学入門』というスゴいタイトルの本を上梓しました。そのほかの著書に、『論理学をつくる』『知識の哲学』『「科学的思考」のレッスン』『科学的実在論を擁護する』『恐怖の哲学』など。
関連書籍

