
「思考入門 “よく考える” ための教室」第9回(最終回) 〔ガクモンのススメ・ヌーボー〕 戸田山和久(文と絵)
みなさんお楽しみの「思考入門」、いよいよ大団円をむかえます。つまりは今回が最終回ってことで、戸田山さん気合入ってますよ~。生まれながらの「アホさかげん」を乗り越える究極の方法、最後にキチっと教えてくれます。そして、最後の最後は「トダヤマ流・ガクモンのすすめ」の登場、大感動の幕切れです。でもみなさん、不満かもしれませんね~。「ディベートの方法についてもう少し教えてほしかった」「ライティングのやりかた、ちっとも書いてないじゃん」……大丈夫ですよ。連載の内容にきっちり加筆したうえで、パワーアップした「思考入門」がもうすぐもうすぐ本になります。そのときまで、ど~か待っててくださいね。はい、それとトダヤマさんの新刊も出ますよ~。タイトルはなんと『教養の書』、2月の28日に全国の書店さんに並びます。「思考入門」の姉妹編、みなさんこちらもぜひ読んでくださいね。はい、最終回ということで前フリも長くなりました。それではみなさん、単行本『思考入門』(仮題ですよ)が出るまでのあいだ、しばしのお別れです。サヨナラ、サヨナラ、サヨ~~ナラ。
思考の拡張手段としての「ガクモン」
ここまで、私たちが生まれながらのアホさかげんをのりこえる二つのやりかたを紹介してきた。「みんなで考える」と「テクノロジーを使う」だ。ガクモンというものは、この二つのやりかたをうまく組み合わせて、人類の思考能力をとんでもなく拡張したものだと言ってよいだろう。というわけで、三つ目のやりかたは「ガクモンに助けてもらう」になる。
ここで言うガクモンは、「科学」と言ってもいいんだけど、日本で「科学」と言うとどうしても、物理学とか化学とか生物学といった「自然科学」を思い浮かべてしまう。経済学とか心理学、社会学などいわゆる「文系」の、「社会科学」「人文科学」も区別しないで話をしたいので、ひっくるめて「ガクモン」と呼んでおこう。
すでになんども繰り返してきたことだけど、ガクモンはひとりじゃできない。たくさんのひとの思考をうまく集めないとできない。しかも、ただたくさん集めただけでは、集合愚になってしまうかもしれない。じょうずに集めて、じょうずに仕事を分担する必要がある。ガクモンはそのためのさまざまなテクノロジー(人工物)を編み出して取り入れてきた。そのなかでも、いちばん大事なのは「制度」だ。
査読〈さどく〉制度って知ってるかい?
たとえば、論文。いいことを思いついたり、新しいことを発見したら、論文に書いて発表しなければならない。これがガクモンのルールだ。ずっと自分の頭のなかだけに隠しておいて、自分だけの利益のために使おう、ということはゆるされない。だいいち、そうしている間に、ほかのひとも同じことを見つけて、先に発表してしまうかもしれない。ということは「競争」も捨てたモンじゃない。学者たちに競争させ、一番乗りしたひとには名誉が与えられる(たとえば、賞をもらったり、発見したものやことがらに自分の名前をつけてもらえるとか)。これは、新しいアイディアを考え出すのを促し、貴重な知識をひとりじめさせないで、みんなでシェアすることで、さらに先へ進む役に立っているんだ。
最近では、この競争が行きすぎて、逆にいろんな弊害が生まれてきている。論文の数ばかりで研究者が評価されるので、読み切れないほど論文が書かれるようになったり、自分の論文数を増やそうと研究不正が横行したり。でも、そもそもはガクモンの世界に競争があるのは、ガクモンがじょうずにひとびとの思考を集めて使っていくために編み出された有益なしくみなんだ。
それから、査読。学者は、ほかの学者が書いた論文を、たいていの場合は信頼する。疑い深いこと──通説を鵜呑〈うの〉みにするのではなく、いちどは疑ってみることはガクモンをするうえでよいことなのだけど、度がすぎるとかえってよくない。仲間のやってくれたことをいちいち疑っていると、ガクモンを先に進めることができないからだ。この論文に書いてあることは本当だろうか、よし、自分で実験をやり直してゼロから確かめてやれ、ってのは時間の無駄づかいだ。もちろん、ものすごい大発見やびっくりするような結果については、追試とか再現実験とかいって、みんなで同じ結果が出るかを確かめることもある。でも、それほどビックリでもない結果は、基本的には信用して進んでいく。
どうしてこういう信頼が成り立つんだろう。論文の信頼性を保つためのしくみがあるからだ。査読制度と呼ばれている。学術雑誌に投稿された論文はそのまま掲載されるなんてことはまずない。「ほかのひとの論文の焼き直しではないだろうね」「どうでもいいような結果ではないだろうね」とか、「ちゃんとした実験がおこなわれているか」「得られた結果の解釈は正しいか」「主張に十分なサポートがあるか」など、同じ研究分野の複数の学者によっていろいろな観点からチェックされる。不十分と判断されると掲載されない。あるいは、書き直しを命じられる。えこひいきや逆に差別があるといけないので、誰が投稿した論文なのか、誰が査読しているのか、どちらにもわからないようにしてある。
こうした、けっこう厳しい査読をくぐり抜けたものだけが論文として掲載される。だから、学者はほかのひとが書いた論文を信用しているんだ。ネット上のブログやツィートとはまるで違うね。
制度に縛〈しば〉られているからこそ、思考が拡張するんだ
さて、査読制度が成り立つためには、査読をする側もされる側も、その基準についてだいたい合意していないといけない。つまり、どういう実験をどのくらいちゃんとやればいいのか、得られたデータをどういうふうに解釈すればいいのか、どのくらいの誤差があっていいのか。ひっくるめて言えば、主張したいことがらにどのくらい強いサポートがなければいけないのかについて、両者がおおよそ同じ基準をもっていなければならないということだ。で、こういうサポート基準は、「方法論」と呼ばれるもののいちばん大事な要素だと言える。
こうした基準は、学問分野ごとにちょっとずつ違う。ときには、一つの学問分野のなかで、基準が変わることだってある(たいていは厳しくなる方向に変わる)。
たとえば、2016年に、アメリカ統計学会は、いろんな分野で「p値」という統計学上の数値基準が正しく使われていない、つまり乱用・誤用されているという声明を出した。これをうけて、p値を使いまくっていた心理学などの分野では、基準を変えようという動きが出てきた、なんてことが起きたりする。
ある分野の学者になる、ということは、こうした制度を受け入れることと、それを支えているその分野の最新の「方法論」を身につける、ということ。ここで大事なのは次のことだ。どっちも、「こうしなさい」とか「これしちゃダメ」というきまりなので、キミをある意味で束縛〈そくばく〉するものだ。でも、その束縛を受け入れることで、キミはたくさんの学者たちを仲間にすることができ、ガクモンによってキミの思考を大きく拡張することができる。まず、確認しておこう。ガクモンは人類が開発してきた思考拡張の最終兵器だ。だから、学ぶべきなのである。
ガクシャにならないキミにガクモンはいらないのか?
とはいえ、次のような反論がありそうだ。でも、これって将来学者になるひとに限った話でしょ。ボクは学者になんかならないから、思考拡張の最終兵器かどうかしらないけど、そんなものを身につける必要もないし、だいいちできそうにないよ。──いや、そうでもないと思うんだ。ガクモンは専門の学者にならないひとにも役立つ。しかも、思考の拡張手段として。このことを確認しておこう。
キミたちが学校で教わるのは、たいてい過去のガクモンがすでに明らかにしてくれたことだ。こうした知識を身につけることによって、キミはそれまで考えられなかったことが考えられるようになる。
雷は空中放電だということを学ぶ。つよい電気は空気中を流れることがあるということを知る。そうしたら、自撮り棒を電車の高圧電線に向けて突き出すともしかしたらアブないんじゃないか、と考えることができるようになる。プラットホームで自撮り棒を電線に向けてはいかんよ、と張り紙がしてあるけど、あれってたんなるマナーをキミに押しつけているんじゃないということがわかる。
こうしてガクモンの成果である知識を身につけることによって、キミは思考を拡張でき、そして自分の命を守ることができる。これはわかりやすいね。
だけど、私がもっと強調したいのは次のことだ。キミは、ガクモンの結果わかった知識を学ぶだけではなく、ガクモンのやりかたを身につけることによって、もっともっと自分の思考を拡張することができるんだ。でも、ガクモンのやりかた、いいかえればガクモンの手続き・方法って、学校ではあまり教えてくれない。地球の周りを太陽が回っているんじゃなくて、太陽の周りを地球が回っているって教わるでしょ。でも、どうやってそれがわかったのかは教えてくれない。もしかしたら、奈良時代より前には「はひふへほ」は「ぱぴぷぺぽ」と発音されていたと教わったかもしれない。でも、それがどうやってわかったのかは教わらなかったろう。
どうしてそれがわかったんだろう、どうしてそう言えるんだろう、と考えること。そしてそれを尋ねたり、調べたりする姿勢をもつこと。これがガクモンのやりかたを身につける第一歩だ。そしてそれは学者にならないひとにとってもたいせつなことだ。なぜなら、ガクモン的なやりかたは、キミの思考能力をうんと高めてくれるから。じゃあ、「ガクモンによって拡張された思考」、つづめて言えば「ガクモン的思考」ってどういう特徴をもっているのだろう。
じつは、「ガクモン的思考」(世の中では「科学リテラシー」とも言われる)ってどういうものか、なぜ専門家じゃないひとにもそれが大事なのかについては、私はもう本を書いている。『「科学的思考」のレッスン』(NHK出版新書)だ。くわしいことはそちらの本を見てもらうことにして、ここでは、この本では書かなかった(そのときははっきり気づいていなかったので)、ガクモン的思考のたいせつな特徴について話をしよう。そのために、ちょっと脱線する。でも、じきに本筋にもどるから安心して。
鍋奉行〈なべぶぎょう〉の憂鬱〈ゆううつ〉
「鍋奉行」という言葉を知ってる? みんなで鍋料理を囲んでいるとき、かならず現れるお節介やきのことだ。こういうひとはやたらと仕切りたがる。「ほら、そこのエビ、火が通ったから食べて。早く食べないとかたくなっちゃうよ」とか。しまいには、誰も頼みもしないのに取り分けようとする。こういうヤツは、焼き鳥屋では、鶏肉を串から外してバラバラにしちゃう。「はい、ひとり2個ずつね」とか言って。あーうっとおしい。
なので、鍋奉行を困らせてやろう。というので次のパズルを考えた。キミが鍋奉行体質のひとだとしよう。キミを含めて何人かで寄せ鍋パーティをやっている(人数はわからない)。パーティの参加メンバーについて、次のことがわかったとしよう。
(1)鶏肉の嫌いなメンバーはみなシイタケも嫌いである
(2)シイタケが嫌いで鶏肉の好きなメンバーはいない
これだけの情報から確実に言えることは、次のうちどれだろう。ただし、好きの反対は嫌い、嫌いの反対は好き、とする。つまり、好きでも嫌いでもない、どっちでもいい、というのは「なし」で考える。話を簡単にするためだ。
(a)鶏肉の好きなメンバーがいるとしたら、そのひとはみなシイタケも好きである
(b)鶏肉が嫌いでシイタケが好きなメンバーがいる
(c)すべてのメンバーは鶏肉が嫌いかシイタケが好きかのどちらかである
まず、(a)はどうだろう。(2)により、鶏肉好きでシイタケ嫌いというひとはいないのだから、鶏肉好きは(もしいるなら)みんなシイタケ好きだ。だから、(a)は確実に正しいと言える。この調子でほかの二つを検討していくことも、もちろんできる。だけどそんなに簡単じゃないよ。だいいち、能率が悪い。(a)(b)(c)3ついっぺんに判定する方法はないだろうか。
ここで図の出番だ。いま、好き嫌いが問題になっているのは鶏肉とシイタケの2つだから、それぞれの好き嫌いの組み合わせは4通りある。(1)(2)はどんな組み合わせの人がいないか、を述べている。(2)は「シイタケ嫌い+鶏肉好き」がいないと言っている。左下の欄に属するメンバーはいないということだ。だからここを塗りつぶしてしまおう。(1)もじつはどういうメンバーがいないかを述べている。「鶏肉嫌いはみんなシイタケ嫌い」ということは、「鶏肉嫌い+シイタケ好き」がいない、ということだ。だから、右上の欄を塗りつぶす。そうすると、こんな図ができる。
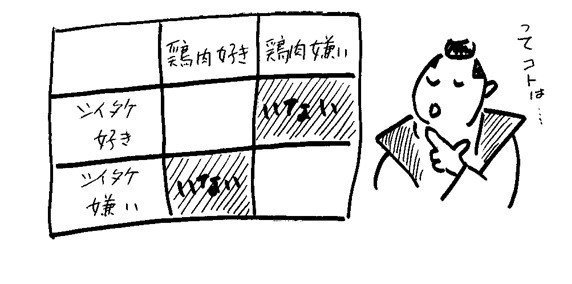
塗りつぶされたところに当てはまるひとはいない。そうすると、(a)鶏肉の好きなメンバーはみなシイタケも好きであるは正しい。(b)鶏肉が嫌いでシイタケが好きなメンバーがいるかどうかはわからない。なぜなら、わかったのは黒いところには誰もいないということだけで、メンバーが二箇所の白いところのどこにいるのかはこれだけの情報からはわからないからだ。全員、左上にいるかもしれないし、全員が右下にいるかもしれない。左上と右下の両方に何人かずついるかもしれない。なので、(b)は(1)(2)から確実に言える、わけではない。(c)は確実に言える。すべてのメンバーは左上か右下のどちらかにいる。左上ならシイタケ好き、右下なら鶏肉嫌いだ。
どうだろう。うまい図を工夫することで、効率的に正確に考えることができるようになった。この図のポイントは、四角を4つの領域に分けて、どこにひとがいないか、いるとしたらどこかという情報を書き込んでいくことだ。大事なのは4つの領域に分けることだけなので、それさえやってくれるなら別の図でもいい。キミたちはきっとベン図を習ったろう。
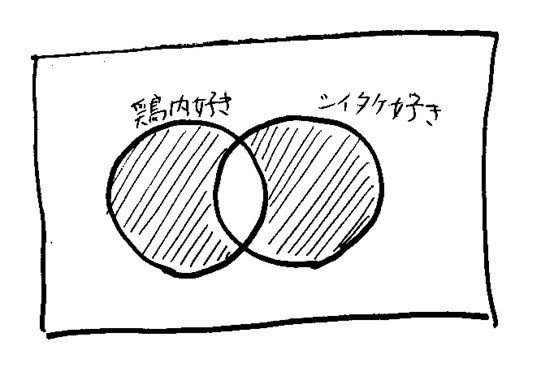
でも、私はさっきの図のほうがわかりやすいと思う。なぜなら、ベン図では、「シイタケ嫌い+鶏肉嫌い」を表す領域が、2つのマルの外側の穴の空いた形になるからだ。4つの組み合わせを表す図形ができるだけ同じ形で、できれば同じ大きさのほうが考えやすいんだ。
エビ様お成り~、するとどうなるか?
ところで、シイタケ鶏肉鍋はちょっとさみしい。そこでエビもいれてあげよう。だんだん豪華になってきたぞ。そうするとエビの好き嫌いも考えてあげなければいけない。そこで、さっきの(1)(2)に加えて、次の2つの情報が分かったとしよう。
(3)エビが好きなメンバーがいるとしたら、そういうひとは全員シイタケが嫌い
(4)エビも鶏肉もシイタケも嫌いなメンバーはいない
そして、キミの鍋奉行ぶりもエスカレートして、ついに取り分けの境地に達したとしよう。さて、このときどのような組み合わせで取り分けてあげればよいだろう。つまり、誰も手を伸ばさないと最初から分かっている組み合わせはどれで、誰かがとってくれそうな組み合わせはどれだろう。
(a)エビのみ (b)エビ+シイタケ (c)エビ+鶏肉 (d)シイタケ+鶏肉
こんどはエビ、シイタケ、鶏肉の3品について、好きと嫌いを考えることになるから、ぜんぶで8領域に分割すればよい。ベン図なら簡単で、
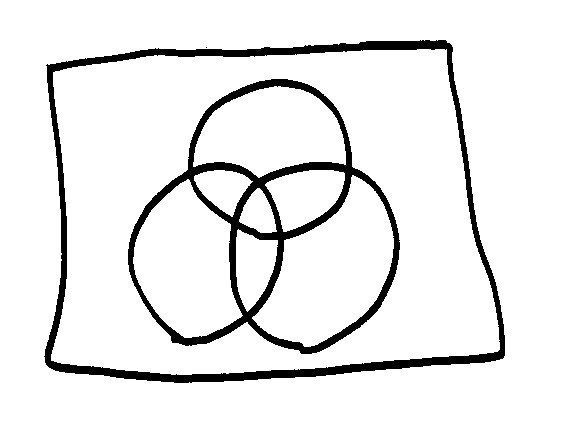
こうやればよい。じゃあ、さっき私がオススメしたやりかただったらどうなるだろう。これもちょっと工夫すればよくって、次のような図を描くことができる。
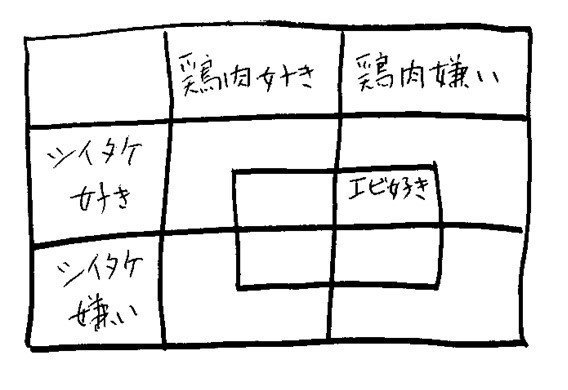
真ん中の四角のなかはエビ好き、外側がエビ嫌いを表す。ここに(1)(2)(3)(4)の情報を描き込んでみると次のようになる。黒いところは、そういう組み合わせの好き嫌いをもったひとはいない、ということを表す。
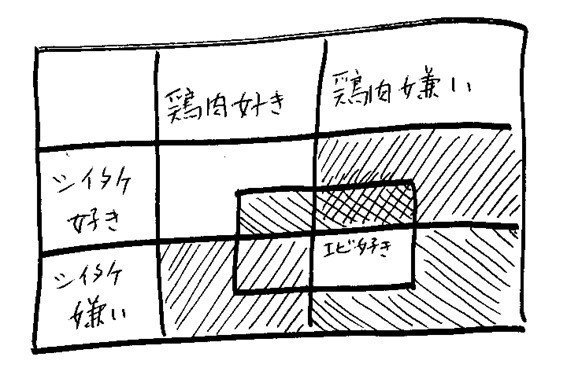
そうすると、一目瞭然。このグループには、「鶏肉好き+シイタケ好き+エビ嫌い」か「鶏肉嫌い+シイタケ嫌い+エビ好き」の2種類のひとしかいない。だから、「(b)エビ+シイタケ」「(c)エビ+鶏肉」を残さず食べてくれるひとはいない。誰かが残さず食べてくれそうなのは(a)と(d)だけだ。
8つの領域ができるだけ同じ形と大きさであって欲しかったんだけど、それはちょっと無理だった。でも4つずつ同じ形と大きさなので、それでもベン図よりは考えやすい。もちろんベン図でもいいんだけど。
ハクサイくん参加で可能性は16通り!
じゃあ、もう一品加えたらどうする。ハクサイの好き嫌いも聞いちゃおうというわけだ。こうなると、もうベン図では手に負えなくなる。そうなの? こんなふうに描けばいいんじゃない、と言うかもしれない。
でも、試しにこの図を描いてごらん。4つの円をこんな具合にきれいに重なるように描くことじたいが至難の技〈わざ〉だし、これではまだ14通りにしか分かれていない。
ポイントは、16通りの組み合わせを表す領域を、できるだけ同じ形と大きさで図示することだ。たとえば次のようなのはどうか。
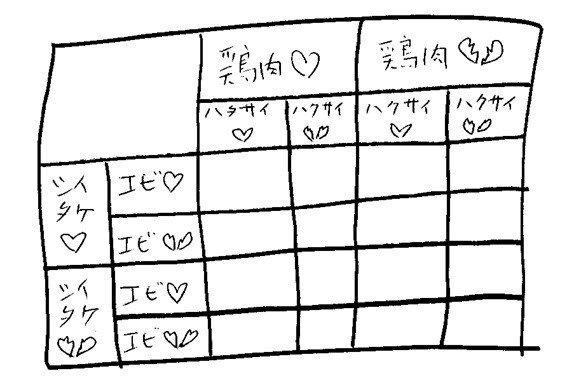
残念ながら、こんどはエビとハクサイの好き嫌いを表す領域が、それぞれ2つに分かれてしまっている。たとえばエビ好きは1行目と3行目に分かれている。でも、塗りつぶすときに塗り残しがないように気をつければ、これでもなんとか使い物になる。けっこう実際の役に立つよ。
図とことば
以上でわかったことをまとめるとこうなる。前回、私たちの思考を拡張する最も大切な人工物として「ことば」の役割を強調した。ことばは、何かを表すはたらきをもったもの、つまり表象〈ひょうしょう〉の代表選手だ。そして表象のもうひとつの代表例が絵とか図なのである。ことばは思考能力を増強する。同じくらい、図も思考能力を増強してくれる。
どっちのほうが思考能力増強装置としてすぐれているか、と問うのはナンセンス。それぞれ得意なところと不得意なところがある。たとえば、「郵便局の向かって右側にクリーニング店があり、郵便局の向かって左側に喫茶店がある」ということから「クリーニング店の左側に喫茶店がある」ということを推論するのを、ことばだけを使ってやれ、と言われるとすごく難しい。でも、三つの店を図に表せば、クリーニング店と喫茶店の位置関係は一目でわかる。図は、推論を自動的にやってしまう。
だけど、こんどは与えられた情報が、「郵便局の向かって右側にクリーニング店があり、郵便局の向かって右側に喫茶店がある」だとしよう。そもそもこの情報をひとつの絵に描くことができない。郵便局を左端に描くのはいいとして、クリーニング店と喫茶店をどの順番で並べればいいかわからないからだ。こういう決まらないところ、不確定なところがある情報も、ことばでなら難なく表せる。図や絵はこうしたことには不向きだ。
というわけで、図はうまく使えば、私たちの思考を、正確に、効率的にしてくれる。ほとんど図のほうで自動的に考えてくれるようなときもある。ことばのレパートリーを増やしてそれを使いこなせるようになるのと同じくらい、図のレパートリーを増やしてうまく使えるようになるのは、思考力を高めるうえで大切なことなんだ。
ツルカメ算必勝法
「役に立つこと」をむずかしく言うと、「効用」ってなるんだけど、図の効用について、もう一つ指摘しておくことがある。キミたちは、ツルカメ算って習った? こんなやつだ。ツルとカメがあわせて8匹います。足はあわせて22本です。ツルとカメはそれぞれ何匹いるでしょうか(ツルの足は2本、カメの足は4本、というのは前提ね)。……じつに不自然な問題だ。ツルとカメがあわせて何匹いるか勘定したときに、それぞれ何匹いるかなんていっしょにわかっちゃうはずだもん。ま、それはおいておいて。
私が小学生のときに教わった解きかたはこういうの。かりに8匹がぜんぶツルだとしよう。そうすると、足は総計2×8=16本のはずだ。でも足は22本で6本多い。この多い分は、カメがいるせいだ。カメの足はツルより2本多い。この余分な2本がつもりつもって6本の違いになった。ということは6割る2で3匹のカメが含まれていたわけである。ツルは、8−3=5羽。……なんて不自然な解きかた! ツルもカメもいるとわかっているのに、あえてぜんぶツルとしてみる、というのがワザとらしい。私の先生は、カメが前足を引っ込めたとしてみよう、というわけのわからん言い訳をしていた。
あるとき、友だちが塾で教わったと言って、次のようなとき方を教えてくれた。たとえばカメが3匹いたら、足の本数の総計は4×3で12本だ。これって、縦4cm、横3cmの長方形の面積が12平方cmというのと同じ計算だ。ということは、このツルカメ算の問題は、次のような問題に直せる。
高さ4cmと2cmの二つの長方形が図のように置かれています。横の長さはあわせて8cmです。面積はあわせて22平方cmです。それぞれの長方形の横の長さはいくらでしょうか。
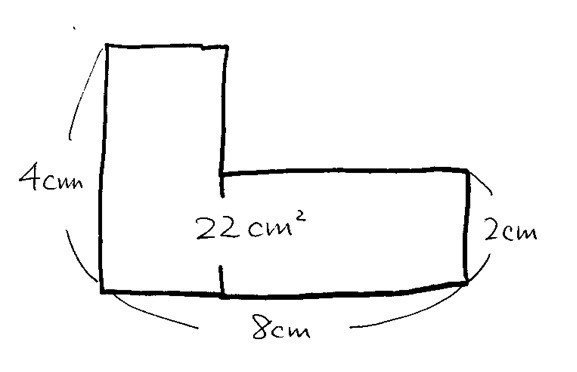
これってすごく簡単。この図形を二つの長方形が横に並んでるのではなく、二つの長方形が縦に積み重なっているように、区切り方を変えて見てみる。下にある長方形の面積は16平方cmだ。そうすると、上に乗っかっている長方形の面積は22-16で6平方cm。この長方形の縦の長さは2cmだから横は3cm。
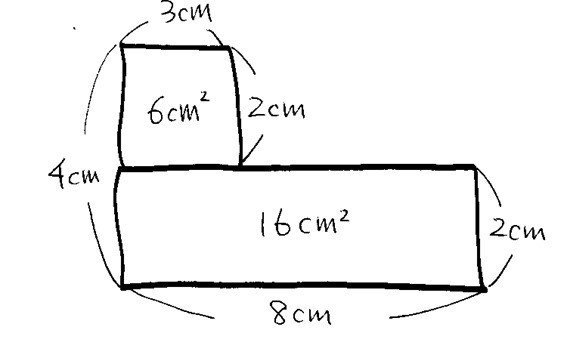
もともとの解きかたで、「ぜんぶツルだとしてみる」というすごく不自然な想定をしていたところが、L字型の図形の区切りかたを変えて見てみる、というすごく自然な操作に置き換えられているんだ。
「何かを図で表す」ってどういうことなんだろう?
私たちが喜んだのも当然だろう。これなら、ツルとカメだけじゃない。ゴキブリスパイダー算でもどんと来いだ。足の本数かける匹数イコール足の総数、だけじゃなく、単価かける個数イコール総額、平均かけるサンプル数イコール総計、食塩水の濃度かける食塩水の量イコール食塩の量、速度かける時間イコール移動距離……こういうかけ算を含む問題はみんな、縦かける横イコール面積の問題に直して考えることができる。1つ4円のキャンディと1つ2円のキャンディをあわせて8個買ったら、22円になりました。それぞれ何個買ったのでしょうか。という問題も同じように解ける。
それは、ツルとカメの問題も、二種類のキャンディの問題も、二つの長方形の面積の問題も、みんな同じ図で表せるからだ。同じ図で表せるということは、3つの問題には何か共通したところがあるということを意味している。ツルの羽根のことや、カメの甲羅〈こうら〉や、キャンディの色や味、長方形の色、そういった「どうでもいいこと」を忘れてしまって、残った何かが共通しているんだ。その共通した何かを「構造」という。
三つの問題は構造が共通している。カメとキャンディと長方形にはどこも似たところがないけど、ツルとカメ(の足)からなる集まり、キャンディ(の値段)からなる集まり、長方形(の面積)からなる集まりになると、共通点が出てくる。それが構造だ。「パターン」と言ってもいいかな。
何かを図に表すということは、どうでもいい細かいことを見えなくして、ある集まり(ガクモンのほうでは「システム」とか「系〈けい〉」とか言ったりする)の構造を取り出すということなのである。
「目を凝〈こ〉らすこと」と「目を細めること」
さ、ようやく本論に戻ることができる。どうでもいい細かいことをあえて見えなくする。そして異なる系が隠しもっていた共通の構造・パターンを見えるようにする。これがガクモンの方法のいちばん大事な特徴なんだ。われわれの脳みそはこれがあまり得意ではない、というかほとんどできない。それをできるように思考を拡張してくれるのがガクモンの意義だ。
ガクモンというと、ひとつのことをどこまでもくわしく調べる、というイメージがあるかもしれない。ニホンザルの群れを研究するのに、一匹一匹に名前をつけて区別して、それぞれの行動を細かに観察するとか。真珠湾攻撃につながる過程で誰がどんな発言をしたのかをちくいち調べ上げるとか。もちろん、ガクモンはこういうこともやる。たとえて言うなら、目を凝らしてうんと近づいて見る、というやりかただ。
でも、そのちょうど逆のこともやる。目を細めて一歩遠ざかって眺める。そうすると、細かなところは見えなくなる代わりに、全体がもっているパターンが浮かび上がってくる。デジタル画像に親しんでいるキミたちは、画像をドンドン拡大していくと、色のついた四角(ピクセル)が並んでいるのが見えるだけで、何の画像なのかわからなくなっちゃったという経験があるだろう。そういうとき、目を細めたり、遠くから見ると、かえって何が写っているのかが見えてくる。
ガクモンの強みは、この両方の見方をできるようにしてくれる、というところにある。普通に目を開いて、中距離から見ていたのでは見えないものを見せてくれる。それがガクモンの意義だ。
図の効用と数学の効用は、じつは似ている
図は「目を細めて一歩遠ざかって眺める」ための手段だ。それのもっと発展したものが何を隠そう数学なのである。中学生になると、方程式というものを教わる。それを使うとツルカメ算はもっと簡単に解ける。ツルカメ合わせて8匹で、かめがx匹、つるがy匹だとすると、
x+y=8
足があわせて22本だから
4x+2y=22
この二つの方程式(こういうのを連立方程式という)を解け、という問題になる。キャンディの問題も、二つの長方形の面積の問題も同じ連立方程式を解く問題になっちゃう。この連立方程式は、3つの問題(ほかのたくさんの問題も含む)に共通の構造を取り出したものになっている。
もう一つ例をあげよう。振り子は重りが行ったり来たりしている。バネの先に重りをつけて引っ張って手を離すと、重りが行ったり来たりする。あるいは、ヒモの先に重りをつけて、同じ速さでぐるぐる回しているのを想像してほしい。これを真横から見ているとしよう。そうすると重りが行ったり来たりしているように見えるはずだ。
じつはこの3つの「行ったり来たり」は、同じ形をした方程式で表すことができる。つまり、共通のパターンをもっているわけだ。だから、ひっくるめて「単振動」と呼ばれる。自然界にある「行ったり来たり」現象のいちばん基本的なものだ。
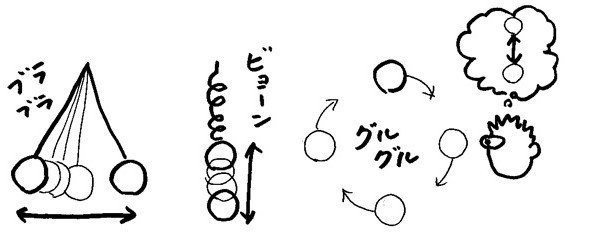
「行ったり来たり」3パターン
というわけで数学も、目を細めて一歩遠ざかって眺め、隠れていた共通の構造を取り出すための有力なツールなんだ。そればかりか、数学は図よりももっと強力だ。何しろ、「絵にも描けない」構造も数学なら表現することができるから。三次元図形、たとえば立方体を紙に描くことはなんとかできる。でも、四次元の立方体を二次元の紙に描くことは難しい。でも、それを式で表現することは簡単だ。それどころか何次元でもOK。情報科学では100次元の空間なんてザラに使う。それどころか物理学、たとえば量子力学では無限次元の空間が出てくる。どちらも図には書けない構造だ。でも、式で表現することは簡単。
数学以外のガクモンは、基本的には「この世にあるもの」を研究している。生物学はユニコーンやドラゴンを調べたりしない。数学は別だ。この世にあるかないかなんてお構いないしに、どんな構造だって調べてしまう、すごく自由なものなんだ。そのために、いろんな構造をうまく記述できるように数学のことばはどんどん拡張されてきた。数学は記述できる構造のレパートリーがものすごくたくさんある。だからこそ、数学はほかのガクモンにもものすごく役に立つんだ。
たとえば、一人ひとりのひとが自分の儲〈もう〉けを増やそうとして、マーケットで取引をしているとき。全体としてどんなパターンが生まれてくるかな、といったことを目を細めて一歩遠ざかって眺めようとするならば、数学を使わないといけない。このように、数学は何を研究するのにも役立つ。というのは、どんなものもパターンや構造をもっていて、その構造を調べるのに数学ほど適したものはないからだ。
……というわけで、ガクモンが私たちの思考を拡張してくれる、ひとつのだいじなやりかたについて話をしてきた。世の中で起きていることを、目を細めて一歩遠ざかって眺め、隠れていた構造を大づかみにする。ガクモンは、こういう思考法を可能にしてくれる、ということだ。
新「学問のススメ」
だから、みんなガクモンを身につけよう。ガクモンは頭の良いひとがやるもんでしょ、というのはまちがっている。勤勉さと、新しい知識とやりかたを受け入れる素直さがあればガクモンは誰にでもできる。
一方で、ガクモンをやると頭が良くなるという言いかたも要注意だ。たしかにある意味で、ガクモンを身につけると頭が良くなる。なぜなら、キミの思考が拡張されるから。でも、キミが生まれながらにしてもっている脳みそじたいが高性能になるわけではない。そうではなく、ガクモンは頭蓋骨〈ずがいこつ〉の外にあるキミの脳なんだ。いわば、キミの脳のアタッチメントだ。
じゃあ、ガクモンというアタッチメントを味方につけて、もっと複雑でもっと普遍的なことをうまく考えられるようになって、何をするのか。つまり、なんのためにガクモンを学ぶのか。こりゃ難しい問いだよね。これまでに数え切れないほどの生徒が数え切れないほどの親と教師に突きつけてきた問いだ。連載の最後に、この難問にこたえるぜ。
なんのためにガクモンするのか。おおそうじゃ『学問のススメ』という本があったな。福澤諭吉の有名な本だ。というわけで読んでみると……がっかりするぞ。だいたいこんなことが書いてあるからだ。
天はひとの上にひとをつくらず、ってんで、ひとは士農工商という4つの身分から解放されて、四民平等〈しみんびょうどう〉の世の中になりました。でも、その建前とはうらはらに世の中にはエラいひととそうでないひと、リッチなひととそうでないひとがいますね。違いはなんでしょう。そうです。ガクモンをやったかどうかですね。四民平等の世の中って競争社会ですよ。そこで生き抜いてエラくなるため、お金持ちになるためには、ガクモンを勉強しましょう。とくにじっさいの役に立つ実学が大切ですよ。
ね、うんざりするような理屈でしょ。福澤諭吉はこれを庶民に向けて書いている。いそいで近代化をとげて欧米列強と肩を並べるためには、国民全体の知的レベルを高めなければ。そのためにはガクモンを身につけてもらわねば。ここまではいいとして、富や名声などの実利を餌〈えさ〉にすれば庶民は勉強するだろうというのが、なんだかひとをバカにしている。だいいち、江戸時代の町民は、寺子屋で読み書きそろばんという実学を学んでいたし、それでがんばって働けば、そこそこおカネもたまったし、家庭ももてたし、それなりに暮らせたんだから。自分の才覚でね。これを読んでそういう庶民が「よしガクモンしよう」ということになったか、はなはだ疑問。
同じことは現代にも当てはまる。競争社会ですよ、厳しいですよ。ガクモンがないと脱落しますよ。ちょっとでもいい大学に行ったほうがお得ですよ。大学でも遊んでいたらダメで、ほんとうにガクモンを身につけて実力をつけないと、会社に雇〈やと〉ってもらえなくなりますよ。出世できませんよ。──こんなんで、若者をガクモンに誘えると考えているとしたら、そりゃかなりアホだ。
だって、「そういう社会にノー!」なひともいっぱいいるわけだから。つまりね、いまある社会でひとを出し抜いてリッチになったり出世したりしたいひとには福澤型ガクモンのススメは有効だ。で、じっさいガクモンはそういうことの役に立つ。いい役立ちかたとは言えないが。
一方、いまある世の中を不満タラタラ受け入れて、自分より弱い者をいじめて憂〈う〉さを晴らして生きていけばいいさ、と思っているひとにはガクモンは役立たない。知恵がつくとかえってツラいからね。自分の信じていたいことを信じていたほうが気が楽だ。
では、いまの世の中、なんのためにガクモンを身につけるのか? いいかえれば、どんなひとにガクモンは役立つんだろうか?
ガクモン──それだけでなく、思考を拡張する人工物をフルに生かしていけるのは、世の中をちょっとでも良い方向に変えたい、世の中を良くすることで自分の幸せを(そして周りの人たちの幸せも)実現したいと思っているひとだけだ。で、こういう若者がたくさんいることを私は知っている。だから、ぜひガクモンをやってくれたまえ。ガクモンを身につけて、キミの思考力という武器を最大限に拡張して闘ってくれたまえ。
了
プロフィール
戸田山和久(とだやま・かずひさ)
1958年、東京都生まれ。発行部数24万部突破のロングセラー『論文の教室』、入門書の定番中の定番『科学哲学の冒険』などの著書がある、科学哲学専攻の名古屋大学情報学研究科教授。哲学と科学のシームレス化を目指して奮闘努力のかたわら、夜な夜なDVD鑑賞にいそしむ大のホラー映画好き。2014年には『哲学入門』というスゴいタイトルの本を上梓しました。そのほかの著書に、『論理学をつくる』『知識の哲学』『「科学的思考」のレッスン』『科学的実在論を擁護する』『恐怖の哲学』など。
関連書籍

