
「思考入門 “よく考える” ための教室」第3回 〔論理的思考には勇気がいるんだ〕 戸田山和久(文と絵)
はいこんにちは。みなさん、夏休みいかがでしたか? いっぱいいっぱい楽しんだでしょうね。はい、9月からは勉強の季節。思考入門もエンジンかけますよ。「論理的に考える」ってどういうことかが3回目のお題です。みなさん、いっしょけんめい考えて相手を説得しようとしても、「ヘリクツ言うな!」ってオコられちゃうことありますね。じゃあ、「ヘリクツ」にならないためには、どうすればいいんでしょう? 戸田山さん、教えてくれますよ。はい、今回の原稿はなんとロンドンから送られてきました。お楽しみのご旅行なのか、お仕事の出張なのか、何度聞いても戸田山さん教えてくれません。やっぱ、怖いコワ~い人ですねえ。はい、時間来ました。今回も楽しんでくださいね。いやあ~、哲学ってホントにいいもんですね。
「論理」という漢字の成り立ちを調べると……
前回の結論はこうだった。「なぜなら」とか「だから」という言葉であらわされる根拠・帰結関係でいくつかの考えをつなげたものを「論理的思考」という。そして、「論理的に考える」とは、考えと考えを根拠・帰結関係でつないで考えていくことだ。そうすると、考えや、その考えをあらわす文をただ一つだけ取り出して、「これって論理的ですかね」と問うても意味がないということになるね。「広島といえばカキですね」は論理的な文でしょうか、ってナンセンスだ。論理はいくつかの文と文との関係について言われる。
「論理」という漢字の成り立ちを振り返ってみると、このことがよくわかる。まずは「論」の方から。「言」つまりごんべんがついているから、言葉に関係していることがわかる。つくりの「侖」はどういう意味だろう。他にこのつくりをもった字は、と探すと、「輪」「倫」「淪」などがある。「淪」って「さざなみ」のこと。「侖」の「冊」みたいな部分を見てみよう。4本の縦棒は、竹や木の細長い板をあらわす。横棒はそれを紐〈ひも〉で結びつけているようすをあらわしている。紙が発明される前は、こういう竹簡〈ちくかん〉・木簡〈もっかん〉と呼ばれるものに字を書いていたんだ。「侖」では、この竹簡・木簡をあらわす部分の上に、さらに横棒があって、その上に「へ」みたいな部分がある。これはどちらも「集まってますよ」ということを強調するためにある。つまり、同じような形をしたもの(同じ種類のもの)が多数集まっているようすをあらわすのが「侖」だ。
自転車の車輪を思い浮かべてごらん。まんなかの軸に向かってたくさんの車軸(スポーク)が集まっている。そこに、にんべんがついた「倫」は、人がたくさん集まってつくられる「世の中」のことだ。さんずいがついた「淪」つまりさざなみは、小さな波がたくさんきれいに並んでいる。というわけで、「論」は言葉がたくさん集まったもの。あるいは文が並んでつくっている集まりをあらわしている。
それじゃ、「理」の方はどうか。「王」はおうへんと言う。王様に関係するのかと思いきや、これは「玉」なのだ。「玉」といえば宝石や貴重できれいな岩石のこと。瑠璃〈るり〉はサファイア。玻璃〈はり〉はガラス(昔は貴重品)。琥珀〈こはく〉、珊瑚〈さんご〉、瑪瑙〈めのう〉。みんなおうへんがついている。「環」とか「球」は、こういう石で作った装身具の形をあらわす。おもしろいのは「班」だ。刀をあらわす「リ」が宝石の間にめりめりと入り込んでいる。鋭利な刃物で貴石を二つに割っているところだ。だから「分ける」という意味になって、グループ分け、つまり班活動の「班」になった。
そういえば、「珈琲〈コーヒー〉」なんていう当て字もあるね。コーヒー豆がいかに高級品だったかがわかる。
では「理」はどういう意味か。これも宝石に関係あるのか。宝石や岩石の名前でこの字を含んでいるものはあるかな。「大理石」が浮かんでくるだろう。「理」は宝石や岩石のもつ「すじ状の模様」をあらわしている。大理石はきれいなすじめ(マーブル模様)が特徴の石でしょ。
だとすると、「論理」は、「言葉の集まり(論)がもつすじめ(理)」つまり「文の集まりがもつすじみち」という意味になる。ほら、やっぱり文の集まりが考えられていて、その文と文をつなぐものが論理ということになるでしょ。
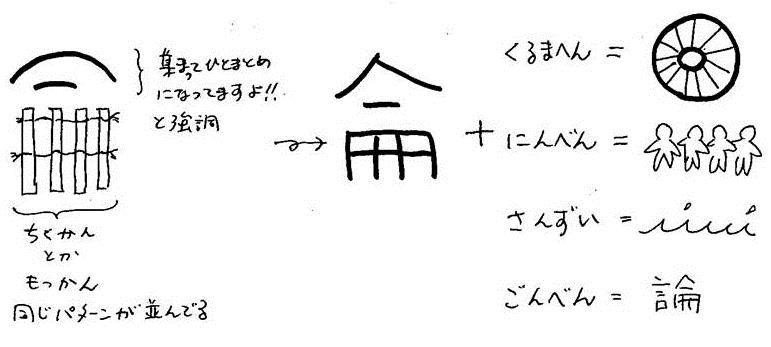
これが「論」の字の成り立ちだ!

「理」の字については、大理石の写真を見てチョーダイ
ポイントは「サポート関係」
「論理」は考えと考え、あるいはその考えをあらわす文と文との関係のあり方だ、ということを確認して、次に進もう。いくつか言葉を整理しておいた方がよさそうだからだ。前回と同じ例を使う。
ぼくはカキが好きじゃない→なぜなら→カキは見た目が気持ち悪いから
カキは見た目が気持ち悪い→だから→ぼくはカキが好きじゃない
これは論理的つながりのいちばん単純でわかりやすい例だ。ふつう「ぼくはカキが好きじゃない」は判断とか主張、「カキは見た目が気持ち悪い」は、判断・主張の根拠とか理由と呼ばれる。また、「なぜなら」の代わりに「というのも」、「だから」の代わりに「ゆえに」とか「したがって」なども使われる。同じことを言うのに何通りもやりかたはあるからね。
1)判断・主張→なぜなら・というのも→理由・根拠
2)理由・根拠→だから・ゆえに・したがって→判断・主張
さらに、2)のような順序で並んでいるとき、理由・根拠は判断・主張のまえに置かれるので、「前提」と呼ばれることもある。そのとき、うしろにくるのは「帰結」とか「結論」と呼ばれる。前提が正しいとしたらどういうことが言えるか、ということだ。
3)前提→だから・ゆえに・したがって→帰結・結論
ややこしいなあ。でも、論理的思考とか論理的文章についての話って、いろんな人がいろんな言葉を好き勝手に使うので、読み手は混乱しちゃう。だから、ここで整理しておくといいかな、と思ったわけ。大事なことは、1)2)3)は、同じことを違った観点から見て、違った言葉を当てはめたものにすぎない、ということを理解しておくことだ。
だとすると、1)2)3)が共通にあらわしている関係そのものを一言であらわす言葉をつくっておくとよいかも。そこで、「サポート関係」という言い方をつかうことにしよう。理由・根拠・前提が判断・主張・帰結・結論を「サポート」する、という具合に使う。
さっきの例の「ぼく」は、じぶんはカキが好きじゃないってことを言いたい。しかし、たんにカキが苦手だと言ったのでは説得力がない。じっさい、「あ、そう。じゃ違うものを注文しよう」と言ってもらえるとは限らない。その前に「え、なんで?」と聞かれる。理由を聞かれるわけだ。言いかえれば、ただ主張するだけじゃなくて、それをサポートしろよ、って要求される。で、この要求に応えるべく「ぼく」が考えたサポートが、見た目がキモいということだったわけ。サポートを与えることで、主張(カキは嫌い)の説得力がちょっとアップする。理由が主張を応援しているみたいな感じ。なので「サポート関係」と呼ぶ。
サポート関係とは、理由・根拠が判断・主張の説得力を高め、前提が帰結・結論の正しさあるいは確からしさを高める、そういう関係だ。そして、「論理的に考える・書く・話す」とは、つねに自分の思考・主張にサポートを与えることに気を配りながら、思考や文をつなげていくことなのである。
ワンタンメン推論とルヴェリエ推論
どういうことをすると、判断・主張・帰結・結論をサポートしたことになるのだろう。じつは、これはいろいろなのね。数学ではふつう「証明」という独特のサポートを与えないといけない。
キミが、3つの連続した数の積はかならず6の倍数になるんじゃないかと気づいたとする。キミはそれを主張する。あるいはそう判断する。そのときに、2×3×4=24、これは6で割り切れる。3×4×5=60も6で割り切れる。4×5×6=120も。5×6×7=210も。8×9×10=720も。「だから」3つの連続した数の積はかならず6の倍数になる。とやったのではサポートしたことにならない。数は無限にたくさんあるので、キミがまだ試したことのない、あるいは一生かかっても計算しきれないようなデカイ数で、キミの主張が成り立たないものがあるかもしれないからだ。
こういうときは、どんな数についても成り立つような「証明」をしなければならない。こんな感じ。
3つの連続した数のうちには少なくとも一つ偶数があるから、それらを掛けあわせたものは2で割り切れる。また、3つの連続した数のうち一つは3の倍数だから、それらを掛けあわせたものは3で割り切れる。「したがって」3つの連続したどんな数の積もかならず6の倍数である。
キミたちの人生で、数学の問題を解くとき以外に、自分の主張にこんなに厳しいサポートを求められることはめったにないだろう。実例をたくさんあげれば、主張をサポートしたことにしてもらえることも多いはずだ。例えば、「この店はワンタンメンが定番みたいだよ」「なんで?」「さっきから入ってきたお客がみんなワンタンメンを注文しているもん」。キミはこの店の客の注文をぜんぶ(創業以来ツブれるまでのすべて)調べたわけじゃないけど、日常生活でキミの主張をサポートするには、これでも十分だろう。じっさい、自然現象や社会現象についての学問的主張の大部分はこんな風にサポートされている。もちろん、実際に調べた実例(サンプル)から、全体の傾向を推測したり、全体の傾向についての主張をちゃんとサポートしたりするためには、統計学というのを学んでもらう必要がある。
こういうサポートのやり方を「帰納〈きのう〉」と言うけど、別にこの言葉を覚えてもらう必要はない。大事なのは、サポートにはいろんなやり方がある、そしてそれは時と場合によって異なる、ということだ。

他にも、こんなやり方もある。現実の科学の歴史から例をとってみよう。1781年に天王星が発見されて、太陽系の惑星は、水星、金星、地球、火星、木星、土星と天王星〈てんのうせい〉の計7つということになった。この直後に、ウルバン・ルヴェリエというフランスの天文学者が、天王星の外側にもう一つ惑星がある、と主張した。キミだって「なんで?」「どうしてそう言えるわけ?」とききたくなるだろう。ルヴェリエがその主張に与えたサポートは次のようなものだった。
じっさいに観測された天王星の軌道は、ニュートン力学をつかって理論的に計算した天王星の軌道と微妙にずれている。これは、天王星の外側にもう一つ未発見の惑星があって、その引力の影響を受けて天王星の軌道がずれているのだと考えるとうまく説明がつく。「だから」天王星の外側にもう一つ惑星があるにちがいない。
これがサポートになっていることはわかるかな。「天王星の外にもう一つ惑星がある」という主張が、それだけでなされたときよりも、そう考えたほうがよい理由、そう考えたくなる理由がいっしょに示されると、この主張の確からしさ・説得力が少しアップしている。こういうサポートを「アブダクション」とか「最良の説明への推論」って言うんだけど、いまはこの名前も覚えなくていいや。

サポートにツッコミを入れてみる
というわけで、サポート関係にはいろんなのがあることがわかった。このうち、数学の証明はすごく強いサポート力の持ち主だ。いったん証明がちゃんとされてしまえば、もうその主張はぜったいに正しいということがわかる。でも、他の種類のサポートにはそこまでの力はない。
たとえば、ワンタンメンの件ではこんなことも考えられる。この店のワンタンメンはじつはあまりおいしくないし、定番メニューでもない。でも、たまたまキミが訪れたときに、全日本ワンタンメン研究会の団体がこの店に来ていた。この研究会は、どの店に入ってもワンタンメンを味見することにしている。なので、次から次へとワンタンメンの注文が続いたのだ。店主もさぞかし戸惑ったことだろう。あるいは、この店はワンタンメンがイチオシだというウソの情報がネットに流れたとかでもよい。
こういうケースも考えられるので、ワンタンメンの場合、キミのあげた証拠・理由はたしかに主張をサポートしてはいるけど、そのサポート力は十分ではなかった。ちょっと確からしくなるけど、それはあくまで「ちょっと」だけ。「ぜったいに正しい」ところまではいかない。
いま、もし全日本ワンタンメン研究会があったら、と考えてみたわけだけど、これは何をしたことになるのだろう。キミが行った論理的思考(論理的推論)のサポート関係をうたがってみたのだ。キミがうちたてようとした理由と判断の間のサポート関係はそれほどのもんじゃないよ、と指摘したわけだ。これをサポート関係への「ツッコミ」と呼ぶことにしよう。
数学の証明は結論をサポートする。この証明にミスがなければ、もうそのサポート関係にツッコミを入れることはできない。これに対して、ワンタンメンケースでは、けっこう強力なツッコミを入れることができる。同じことは、ルヴェリエにも当てはまる。
ルヴェリエは、天王星の外側に惑星がありそうだよと言った。つまりは予言した。じっさい、1846年になってドイツのヨハン・ガレが、ルヴェリエの予測した方向に惑星があることを発見した。これが海王星〈かいおうせい〉だ。ルヴェリエの主張は結果的に大当たりだったわけだが、これはルヴェリエの推論にツッコミどころがなかったことを示しているわけではない。あとでもう一回触れることにするけど、主張がサポートされていることと主張が当たっていることとは、まったく別物なのである。
STAP細胞の場合は……
ルヴェリエの与えたサポートが、数学の場合のようにパーフェクトではなかったことは、次の事例からわかる。予言が当たったことに気をよくしたルヴェリエは、こんどは水星の動きに目をつけた。水星の観測上の軌道も、ニュートン力学によって理論的に計算した結果とズレていたからだ。そこでルヴェリエは、水星の内側に未発見の惑星がありそうだと考え、それに天王星の場合と同じサポートを与えた。今回は自信を高めたのかどうかは知らないが、ルヴェリエはその未知の惑星に「ヴァルカン」という名前までつけた。ローマ神話の火、火山、鍛冶〈かじ〉の神の名前ね(なんせ太陽にいちばん近いことになるので)。西洋では惑星にローマ・ギリシアの神さまの名前をつけるでしょ。火星は戦争の神マルス、木星はいちばん偉い神さまのジュピター、「天王星」もギリシア神話の天の神にちなんだ「ウラヌス」の直訳だからね。
ところが、ヴァルカンの場合は予想が外れた。ご存知のように、いままでそんな惑星は見つかっていない。いまでは、水星の軌道のズレはルヴェリエとは違う仕方で説明されている。聞いたことあると思うけど「一般相対性理論」というやつ。太陽はすごく重いので、相対性理論によればまわりの空間が歪〈ゆが〉む。そうすると太陽にいちばん近いところにいる水星の軌道は、空間の歪みを考えないニュートン力学での計算結果とそぐわない、ということになる。
ルヴェリエの与えたサポートは、天王星の場合は結果オーライだった。だからパーフェクトだったように思えてしまう。しかし、同様なサポートを与えた水星についての主張は結果的に間違いだった。サポートは完璧なものではなかった、ということになる。じつはツッコミどころがあったのである。つまり、相対性理論を考えに入れてないじゃん、というツッコミだ。
だからといって、ルヴェリエが自分の主張の証拠・理由と考えたことがらは主張のサポートになっとらん、とかルヴェリエのサポートは科学的ではなかった、ダメサポートだったと言いたいのではない。正真正銘の立派なサポートだったと思う。アインシュタインが相対性理論を提唱したのは20世紀の初めだ。それより1世紀も昔のひとであるルヴェリエには知る由〈よし〉もない。だから、当時の科学的知識に照らして考えれば、「水星の内側に惑星がある」は「天王星の外側に惑星がある」にひけをとらないよい説明だったのである。
だから、主張が結果的に正しいかどうかと、サポートがきちんとされているかどうかとは区別しないといけない。ちゃんとサポートされていたんだけど、結果的には間違いでした、つまりそれなりの証拠や根拠をともなって主張されていたんだけど、あとで正しくないことがわかった主張はいっぱいある。科学の歴史をひもとくと、そういう「あとから見て間違いだったことがわかった科学的主張」がざくざく出てくる。
これに対して、「結果的に当たっていたんだけど、ちゃんとサポートされずに主張されたことがら」は「あてずっぽ」とか「まぐれ当たり」と同じで、科学の手続きの中には入ってこない。あるいは入っちゃダメだ。
このどちらでもない例もある。小保方晴子〈おぼかたはるこ〉さんという研究者が、論文のもとになる実験データをでっちあげていたことが明らかになって、科学者たちの非難の的〈まと〉になった。STAP細胞という、人体のどんな細胞にもなれる「万能細胞」の作り方を発見したというのだけど、自分の作り方でそういう細胞ができたということの証拠となるはずのデータにインチキがあった。このとき、それでもたしかにSTAP細胞はできていたんです、といくら抗弁〈こうべん〉してもだめだし、「本当にSTAP細胞があるかどうか」を問題にしてもいけない。問題になっているのは、STAP細胞ができたという主張が結果的に正しいかどうかではなくて、小保方さんが自分の主張に与えた「サポート」がまともかどうか、そこに不正が含まれていたかどうかなのだから。
「よく考える」を、より論理的に定義してみよう
というわけで、次のことがわかった。サポート関係は程度の問題である。数学の証明のように、根拠・理由が主張を100%サポートすることもある。根拠・理由が主張をまったくサポートしない場合もある。「根拠・理由」がでっちあげだったり不正を含んでいたり、そもそも根拠・理由を示さないでたんに主張したりするだけ、といったケースがこれにあたるだろう。ほとんどの場合はこの両極端の間にある。根拠・理由は主張を「ある程度」サポートする。主張の信ぴょう性や確からしさをちょっと高め、主張の説得力をちょっと増す。
今回は最初に、「論理的に考える・書く・話す」とは自分の思考・主張にサポートを与えながら思考や文をつなげていくことである、と述べた。これではまだ足りなかったかなと思う。なんでもよいから理由を考えたり言ったりしさえすれば「論理的思考」になる、というのでは安直すぎるからね。「論理的に考える」ことが「よく考える」ことの一部であるなら、なおさらそうだ。「論理的観点からみてよく考えるとはどういうことか」に答えなくてはいけない。そこで、次のように修正しよう。
「論理的観点からみてよく考える・書く・話す」とは、つねに自分の思考・主張にできるだけ強いサポートを与えることに気を配りながら、思考や文をつなげていくことである。
「お前はなぜ人を殺したんだ」「太陽が黄色かったからさ」というのは、たしかに理由を挙げているので、そういう意味(理由に基づいて何かを言ったりやったりする、という意味)では論理的なやりとりと言ってもいいんだけど、「よい」論理的やりとりではない、と言いたくなる。じっさい、こういうのを「不条理」って言うんだし。
次に「ツッコミ」の正体を明らかにしてみよう
ところで、「強いサポート」ってもうちょっとちゃんと言うとどういうことなんだろう。100%と0%の中間ケースでは、サポート関係にツッコミを入れることができる。あなたの根拠・理由は主張をそんなにサポートしていないよ、あるいはその程度のサポートじゃだめだよ、そんなのサポートになってないよというツッコミである。
というわけで、サポート関係の強弱は、それにどのくらい強いツッコミを入れることができるかと「うらはら」の関係にある。不条理殺人のケースでは「太陽が黄色いことが人を殺す理由になるもんか」というツッコミがしたくなるし、そのツッコミの方が強力に思える。そこで、「強いサポート」というのを「ツッコミに負けないサポート」と考えてみよう。
そうすると、サポート関係にツッコミを入れるというのはそもそもどういうことなのかを考えてみる必要がある。その答えはすでに述べてあるのだけど、あらためてちゃんと言っておこう。
2×3×4は6で割り切れる。3×4×5は6で割り切れる。4×5×6は6で割り切れる。5×6×7は6で割り切れる。8×9×10は6で割り切れる。「だから」3つの連続した数の積は6の倍数になる。
これは「3つの連続した数の積は6の倍数になる」にサポートを与えようとはしているのだけど、ツッコミができる。サポート部分に書かれた5つのケースはたしかに6で割り切れる、だからサポート部分が言っていることは正しくとも、まだ試していないすごく大きな数の場合、3つの連続した数を掛け合わせると6の倍数になるかどうかわからない、つまり6の倍数にならないことがあるかもしれない(本当はないんだけど、ないとわかったわけではないので、そういう場合が考えられる)。こういうツッコミだ。つまり、「サポート部分が成り立つが主張・結論部分は成り立たないケース」が考えられるじゃん、少なくともそういうケースがないと言えてないじゃんとツッコんでいるわけだ。
こういう「サポート部分が成り立つが主張・結論部分は成り立たないケース」をサポート関係に対する反例と言うことにしよう。
全日本ワンタンメン研究会が来ていたかも、というツッコミは、キミが見た客が全員ワンタンメンを注文したということは成り立ったとしても、この店のすべて(あるいはほとんど)の客がワンタンメンを注文するということは成り立たないケース、つまり反例を指摘している。太陽の質量による空間の歪み(相対性理論の効果)を指摘するツッコミは、水星の軌道がニュートン力学とずれているということは成り立ったとしても、水星の内側に惑星があるということは成り立たない場合があるでしょ(つまり反例があるでしょ)と言っている。ツッコミとは、サポート関係に対する反例を示すことだ。
ツッコミをコワがると、どうなるか?
ツッコミが反例を指摘することだとしよう。だとしたら、そもそもなんでこういうツッコミができるんだろう。それは、結論・主張で、前提・理由で述べたことを超えた「新しいこと」を言って、その結論・主張をその前提・理由でサポートしようとしているからだ。わかりにくいね。具体例をあげる。
3つの数の積の例では、5つの具体例についての計算結果を理由にして、すべての連続した3つの数の積について主張している。ほら、言っていることが増えている。前提・理由では言われていない新しいことが主張されている。ワンタンメンの例では、キミが今日見た客の注文を理由にして、その店のすべての客の注文について主張してる。これも言っていることが増えている。ルヴェリエの例では、水星の動きについての話を理由にして、未知の惑星の存在が主張されている。ここでも、前提・理由に含まれない新しいことが言われている。
これらの3つに共通しているのは、サポート部分が言っていることより、結論・主張部分が言っていることの方がなんらかの意味で増えている、ということだ。だから、その増えた部分に間違いがまぎれこむかもしれない。これが、サポート部分が正しくても、結論・主張部分がまちがっているケース、つまり反例だ。
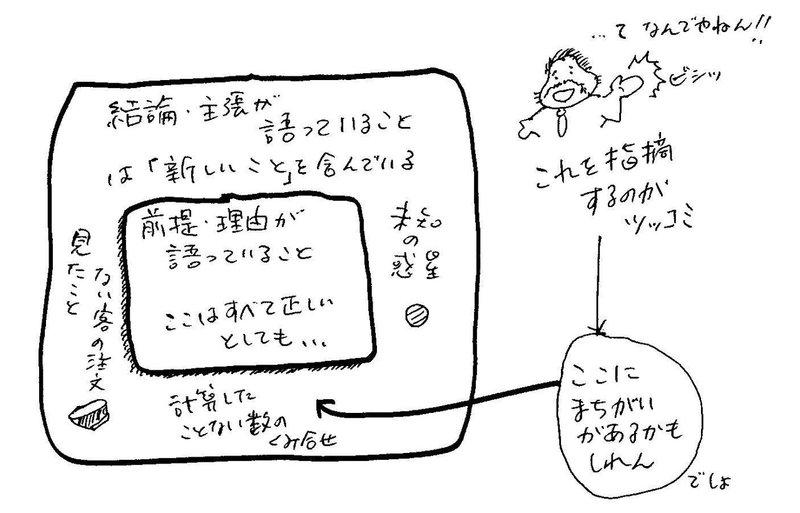
ということは、反例を指摘される、つまりツッコまれるということは、新しいことを言おうとしているということの裏返し、ということだ。ツッコまれる危険を冒さないと新しいことは言えない。だから、逆に言えば、ツッコミをどうしても避けたいなら、何も新しいことを言わなければよい、ということになる。たとえば、次の自称「サポート」を見てみよう。
4)水星の内側にもう一つ惑星がある。なぜなら、水星の内側にもう一つ惑星があるからだ。
5)水星の内側にもう一つ惑星がある。したがって、水星の内側にもう一つ惑星がある。
これ、反例ないのよ。「なぜなら」あるいは「したがって」のまえとうしろに同じ文がある。だから、「サポート部分が正しくて、結論・主張部分がまちがっているケース」はありえない。だって、そんなケースがあったら、同じ文が正しくてまちがっている、ということになっちゃうから。
反例はない。だから、たんに反例によるツッコミを受けるかどうかだけで考えると、これは論理的思考のお手本だということになっちゃう。だけど、これって何も新しいことを言っていないことに注意しよう。サポート部分で言っていることを超えるようなことを何も結論・主張していない(ただ繰り返しているだけだ)から、サポート部分が正しいのに結論部分がまちがっているケースもありえない。
こんな主張にダマされてはいけない!
4)や5)は「同語反復」と呼ばれて、何も言っていないじゃん、という批判の対象になる。4)や5)みたいにあまりにあからさまなのは、すぐにバレるけど、世の中にはけっこう手の込んだ議論がある。たとえば4)や5)のまえとうしろの文をちょっと違った言葉に書き換えると、同じ文ではなくなるのですぐには同語反復に見えない。でも、実は何も言っていない。こういうのって結構ある。あるいは、ぜんたいをややこしくするとバレにくくなる。たとえばこんな風に。
私たちの教祖様は最終解脱者〈げだつしゃ〉だ。なぜなら、そのように経典〈きょうてん〉に書かれているからだ。ではなぜ、その経典を信用してよいのか。それは教祖様がお書きになったものだからだ。ではなぜ、教祖様がお書きになったものは信用できるのか。それは教祖様が宇宙の原理を悟〈さと〉っておられるからだ。なぜ、教祖様が宇宙の原理を悟っておられるのか、それは、教祖様は最終解脱者だからだ。
結局、「教祖様が最終解脱者なのは教祖様が最終解脱者だからだ」とサポートしているわけで、見かけ上同語反復じゃないけど、同じことをやっている。
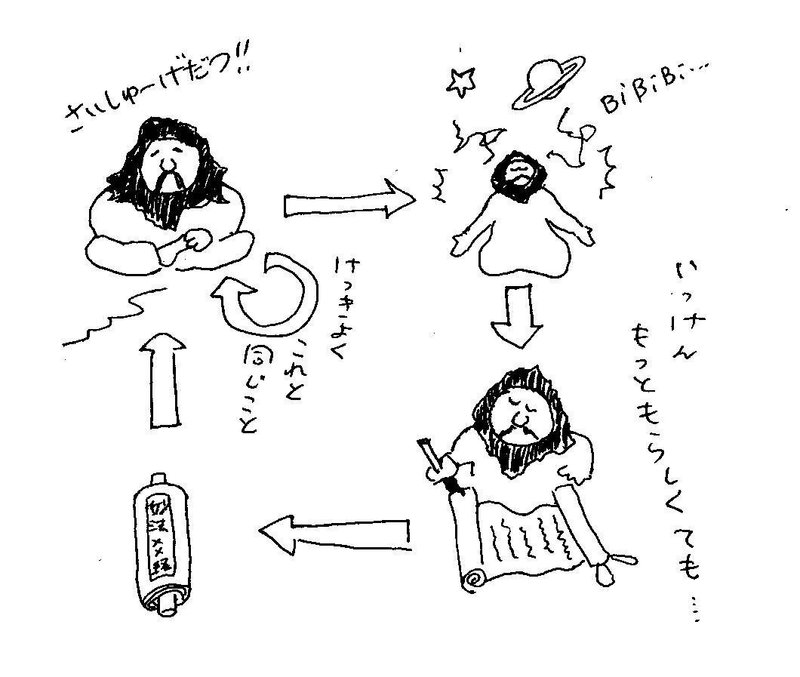
こんなのを「よい論理的思考」とは呼びたくないよね。だから、「よい論理的思考」とは、こういうことになるんじゃないかな。自分がこれまでに知ったこと、考えたことを超えたことがらを主張したり考えようとすること。しかし、それだとツッコミが入る可能性がある。その可能性をひきうけて、できるかぎり強力なツッコミは阻止できるように、サポート関係をしっかりつくりあげながら考えて主張すること。自分の考えにはツッコミが入るということを自覚して何かを言ったり考えたりする、これって臆病者にはなかなかできない。論理的思考には勇気がいるんだ。
了
プロフィール
戸田山和久(とだやま・かずひさ)
1958年、東京都生まれ。発行部数24万部突破のロングセラー『論文の教室』、入門書の定番中の定番『科学哲学の冒険』などの著書がある、科学哲学専攻の名古屋大学情報学研究科教授。哲学と科学のシームレス化を目指して奮闘努力のかたわら、夜な夜なDVD鑑賞にいそしむ大のホラー映画好き。2014年には『哲学入門』というスゴいタイトルの本を上梓しました。そのほかの著書に、『論理学をつくる』『知識の哲学』『「科学的思考」のレッスン』『科学的実在論を擁護する』『恐怖の哲学』など。
関連書籍

